




Next: REFERENCES
Up: Appendix
Previous: New notations and definitions
Given the values of the function 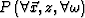 , downward continuation consists of finding the
values of
, downward continuation consists of finding the
values of 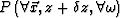 . An expression describing this process lays at the end of the
following proof:
. An expression describing this process lays at the end of the
following proof:
Obtain the Helmholtz equation by applying the Fourier transform
defined by (24) to the wave equation (22) while
taking into account the notation (26) and the property
(25) and rearranging:
| 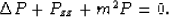 |
(29) |
By derivating relation (28) with respect to x and z we
obtain:
| 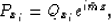 |
(30) |
| 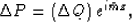 |
(31) |
| 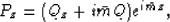 |
(32) |
| 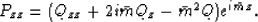 |
(33) |
By plugging into in (29) and eliminating the exponential, we
get:
| 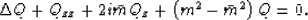 |
(34) |
The second derivative with respect to z can be eliminated by
derivating with respect to z, multiplying by 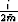 , and
adding the result to (34):
, and
adding the result to (34):
| 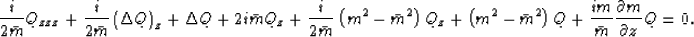 |
(35) |
Note that no approximation has been made between the wave equation
(22) and this point. Eq. 35 is simply the wave
equation in a different coordinate system. Now Qzzz is
approximated by zero:
| 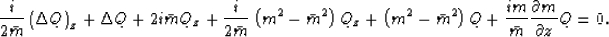 |
(36) |
For the case of a homogenous medium, 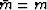 and the equation
turns into the familiar
and the equation
turns into the familiar 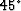 equation:
equation:
| 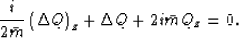 |
(37) |
The 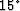 equation is obtained by neglecting the Qxxz term
also:
equation is obtained by neglecting the Qxxz term
also:
| 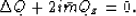 |
(38) |
Downward continuation proceeds by considering
| 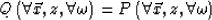 |
(39) |
then by using one of the equations 36, 37 or
38 to find the values of 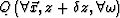 and by finally finding P by undoing
the variable change:
and by finally finding P by undoing
the variable change:
| 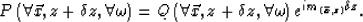 |
(40) |





Next: REFERENCES
Up: Appendix
Previous: New notations and definitions
Stanford Exploration Project
6/8/2002
![]() , and
adding the result to (34):
, and
adding the result to (34):
![]() and the equation
turns into the familiar
and the equation
turns into the familiar ![]() equation:
equation:
![]() equation is obtained by neglecting the Qxxz term
also:
equation is obtained by neglecting the Qxxz term
also:
![]() and by finally finding P by undoing
the variable change:
and by finally finding P by undoing
the variable change: