




Next: Results
Up: Bortfeld's 3 term reflectivity
Previous: Bortfeld's 3 term reflectivity
The basic form just described depends on a 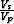 ratio, meaning that to get the information on the rock properties,
you first need a fairly accurate interval velocity model.
Fred Herkenhoff of Chevron realized that by substituting
the value of a stacked trace into the problem, he could constrain
the result to have values similar to those of the stack and remove
the dependence on the velocity ratio. The stack amplitude can be
calculated from the basic form:
ratio, meaning that to get the information on the rock properties,
you first need a fairly accurate interval velocity model.
Fred Herkenhoff of Chevron realized that by substituting
the value of a stacked trace into the problem, he could constrain
the result to have values similar to those of the stack and remove
the dependence on the velocity ratio. The stack amplitude can be
calculated from the basic form:
| 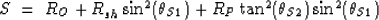 |
(3) |
Here, 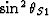 and
and 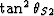 are the averages of
are the averages of
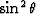 and
and 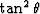 over the range of input angles.
This stack equation is
then used as a substitute for the
over the range of input angles.
This stack equation is
then used as a substitute for the 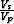 ratio:
ratio:
| 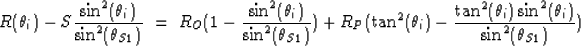 |
(4) |
This form can now be inverted for the zero-offset reflectivity (RO)
and the P-wave reflectivity (RP) without needing the interval velocities.
Once those reflectivities are obtained, the stack equation (Eqn. 3)
can be used to find the gradient term. This inversion is demonstrated in the
next section.





Next: Results
Up: Bortfeld's 3 term reflectivity
Previous: Bortfeld's 3 term reflectivity
Stanford Exploration Project
6/8/2002
![]() ratio, meaning that to get the information on the rock properties,
you first need a fairly accurate interval velocity model.
Fred Herkenhoff of Chevron realized that by substituting
the value of a stacked trace into the problem, he could constrain
the result to have values similar to those of the stack and remove
the dependence on the velocity ratio. The stack amplitude can be
calculated from the basic form:
ratio, meaning that to get the information on the rock properties,
you first need a fairly accurate interval velocity model.
Fred Herkenhoff of Chevron realized that by substituting
the value of a stacked trace into the problem, he could constrain
the result to have values similar to those of the stack and remove
the dependence on the velocity ratio. The stack amplitude can be
calculated from the basic form: