Next: CONCLUSIONS
Up: Berryman et al.: Time-reversal
Previous: TECHNICAL APPROACH
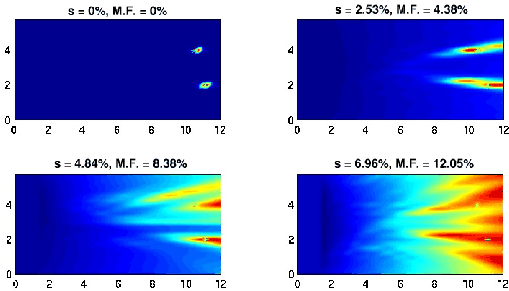
Two_short_MUSIC
Figure 2
The MUSIC central frequency estimate
of the location of two targets in random media with
different strength of the fluctuations of the sound speed. The exact
location of the targets is denoted by green stars
(in the color version). The standard
deviation s and maximum fluctuations (M.F.) are indicated on the top of
each view. The horizontal axis is the range in mm and the vertical axis
is the cross-range in mm.

Examples for frequency-domain MUSIC with two targets are
displayed in Fig.2.
It is clear from this
Figure that no range information is obtained from frequency-domain objective
functionals, and even the cross-range information is often quite
haphazard in random media. Lack of statistical stability prevents
these imaging approaches from being useful in
random media with significant multipathing as
considered here. When the realization of the random
medium is changed, the images obtained typically change also --
which is what we mean by the phrase ``lack of statistical stability'' for
these methods. Note that this approach works well for homogeneous
media, but quickly breaks down when randomness of the velocity field
is important.
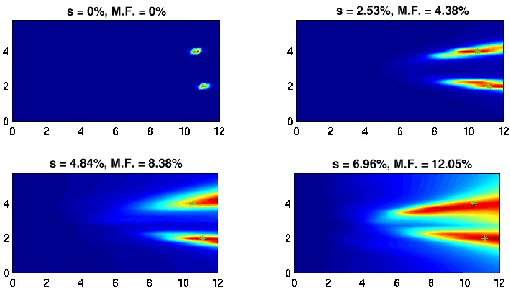
Two_short_DOA
Figure 3
The DOA estimate (5)
of the location of two target in random media with
different strength of the fluctuations of the sound speed. The exact
location of the target is denoted by the green star
(in the color version). The standard
deviation s and maximum fluctuations (M.F.) are indicated on the top of
each view. The horizontal axis is the range in mm and the vertical axis
is the cross-range in mm.

Examples for time-domain MUSIC with two targets are
displayed in Fig.3.
The cross-range results show dramatic improvement
over results using other methods (Berryman et al., 2002).
Range information is still not to be found here, due to loss of
coherence in the random medium; we cannot get exact cancellation
at the targets in this situation whereas coherent refocusing
is possible in homogeneous media.
But the statistical stability of the universal ``comet tails''
-- which was also anticipated by recent theoretical analyses
(Blomgren et al., 2002)
-- is now easily observed.
The images are necessarily shown for specific realizations, but the results
do not change significantly when the underlying realization
of the random medium is changed. This fact has been repeatedly shown
in our simulations, and is the main operational characteristic of
statistically stable methods.
Target localization requires an estimate of the range.
In the far field, only the arrival time information is useful for this
purpose.
Arrival time information is present in the singular
vectors and can also be averaged (for the same random medium)
using the multiple copies available
in the array response matrix for random media -- see Borcea et al. (2002)
-- to obtain very stable estimates of arrival times.
We will now combine this approach with the time-domain
methods to obtain well-localized images of the targets.
For each search point 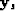 , we compute the objective functional
, we compute the objective functional
| 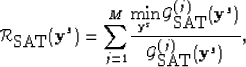 |
(8) |
where
| ![\begin{displaymath}
{\cal G}_{\mbox{SAT}}^{(j)}({\bf y}^s) = {\displaystyle \sum...
... \right\vert^2
\left[ \tau^{(j)}_p - t_p({\bf y}^s) \right]^2. \end{displaymath}](img36.gif) |
(9) |
Here 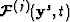 is defined by (Fj),
is defined by (Fj),
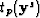 , for
, for 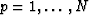 ,
are the deterministic arrival times given by (det-tr-time) and
,
are the deterministic arrival times given by (det-tr-time) and
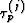 , for
, for 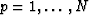 , and
, and 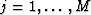 , are the
computed arrival times.
We call (Rsat) the Subspace Arrival Time (SAT) estimator.
, are the
computed arrival times.
We call (Rsat) the Subspace Arrival Time (SAT) estimator.
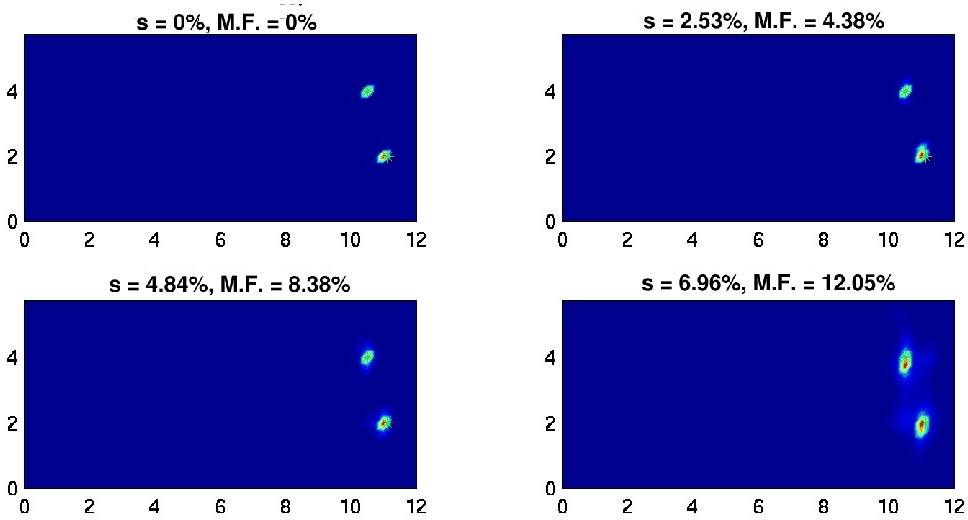
Two_short_SAT-1
Figure 4
The SAT estimate for two targets.

Examples of SAT (or time-domain MUSIC with arrival time estimates from the
averaged singular vectors) for two targets are
displayed in Fig.4. This method is statistically stable and
gives good estimates of the target locations. These localization
results have degraded the least of all those considered
(Borcea et al., 2002; Berryman et al., 2002)
at the highest values of the random fluctuations.





Next: CONCLUSIONS
Up: Berryman et al.: Time-reversal
Previous: TECHNICAL APPROACH
Stanford Exploration Project
6/7/2002
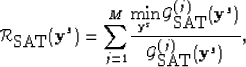
![\begin{displaymath}
{\cal G}_{\mbox{SAT}}^{(j)}({\bf y}^s) = {\displaystyle \sum...
... \right\vert^2
\left[ \tau^{(j)}_p - t_p({\bf y}^s) \right]^2. \end{displaymath}](img36.gif)