In our simulations, the array response matrix ![]() [see definition in (Pt)]
in the frequency domain is symmetric but not Hermitian. In general
(as for array elements with nonisotropic radiation patterns), it is
neither Hermitian nor symmetric, but with slight modifications
our methods apply to this case as well.
The eigenvectors of
[see definition in (Pt)]
in the frequency domain is symmetric but not Hermitian. In general
(as for array elements with nonisotropic radiation patterns), it is
neither Hermitian nor symmetric, but with slight modifications
our methods apply to this case as well.
The eigenvectors of ![]() having unit
norm are denoted by
having unit
norm are denoted by ![]() , for
, for ![]() .The eigenvalues of
.The eigenvalues of
![]() are
are ![]() , with
, with
![]() being the singular values of
being the singular values of ![]() .The significant singular vectors
.The significant singular vectors ![]() [i.e.,
those in the range of
[i.e.,
those in the range of ![]() ] have singular values
] have singular values
![]() for
for ![]() , where M is either
the number of targets, or the size of the array (N) -- whichever
is smaller. We assume that the number of targets is smaller than
the array size N, so that M is in fact the number of
distinguishable targets; this assumption is required by the imaging
methods we employ (such as MUSIC) as will become clear while presenting
the method.
, where M is either
the number of targets, or the size of the array (N) -- whichever
is smaller. We assume that the number of targets is smaller than
the array size N, so that M is in fact the number of
distinguishable targets; this assumption is required by the imaging
methods we employ (such as MUSIC) as will become clear while presenting
the method.
The notation used here is the same as in Borcea et al. (2002).
We denote by ![]() the deterministic
source vector observed at the array for a source located at
the deterministic
source vector observed at the array for a source located at
![]() . Then,
. Then, ![]() is given by
is given by
| |
(2) |
We also define the projection ![]() of
of ![]() onto
the null-space of
onto
the null-space of ![]() by
by
![\begin{displaymath}
\begin{array}
{c}
{\cal P}_N \widehat{\bf g}_0({\bf y}^s,\om...
...f y}^s,\omega)
\right]
\widehat{{\bf U}}_r(\omega),\end{array}\end{displaymath}](img26.gif) |
(3) |
The method we describe here is a time domain variant of
MUSIC (Schmidt, 1979; 1986; Cheney, 2001; Devaney, 2002)
which we label DOA, because
it gives very stable estimates of the direction of arrival.
Frequency domain MUSIC takes a replica (or trial) vector, which is
the impulse response
or Green's function for a point source at some point in the space,
and dots this vector into an observed singular vector at the array.
With appropriate normalization, this dot product acts like a direction
cosine of the angle between the replica vector and the data vector.
If the sum of the squares of these direction cosines is very close to
unity, then it is correct to presume that the source point of that replica
vector is in fact a target location since it lies wholely in the range
of the array response
matrix. Crudely speaking, imaging is accomplished by
plotting ![]() , which will have a strong peak when
the replica source point is close to the target location.
, which will have a strong peak when
the replica source point is close to the target location.
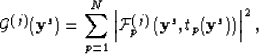 |
(4) |
![\begin{displaymath}
\begin{array}
{ll}
\hbox{\boldmath{${\cal F}$}}^{(j)}({\bf y...
...omega) \right]
\widehat{{\bf U}}_r(\omega) d \omega,\end{array}\end{displaymath}](img30.gif) |
(5) |
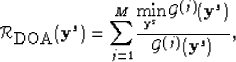 |
(6) |
The arrival time ![]() is the deterministic travel time
from the p-th
transducer to the search point,
is the deterministic travel time
from the p-th
transducer to the search point,
| |
(7) |