




Next: Dealing with sparse data
Up: Lomask: Madagascar
Previous: Looking at data-space
We used the first derivative in our fitting goal to remove the shifts between tracks. As was done previously in Lomask (1998), I tested the nature of the residual by estimating a 1D PEF on it, to see if correcting the weighting operator made difference. If the estimated PEFs are not first derivatives, then we would want to use one of them in our fitting goals instead of 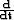 . The PEFs look like first derivatives, but in the case of the PEFs with more than three terms, it isn't obviously a first derivative. We will need to look at the impulse response of the inverse PEF to get a better idea of the nature of the PEFs.
. The PEFs look like first derivatives, but in the case of the PEFs with more than three terms, it isn't obviously a first derivative. We will need to look at the impulse response of the inverse PEF to get a better idea of the nature of the PEFs.
| PEF |
|
Coef 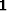 |
Coef 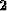 |
Coef 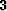 |
Coef 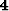 |
Coef 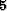 |
|
|
|
|---|
| 2 terms |
|
1.00 |
-1.00 |
- |
- |
- |
|
|
|
| 3 terms |
|
1.00 |
-1.06 |
0.055 |
- |
- |
|
|
|
| 4 terms |
|
1.00 |
-1.08 |
0.497 |
-0.419 |
- |
|
|
|
| 5 terms |
|
1.00 |
-1.08 |
0.284 |
-0.258 |
0.050 |
|
|
|
| 10 terms |
|
1.00 |
-1.07 |
0.270 |
-0.227 |
0.028 |
|
|
|
| |
|
-0.019 |
-0.014 |
0.001 |
-0.035 |
0.053 |
|
|
|





Next: Dealing with sparse data
Up: Lomask: Madagascar
Previous: Looking at data-space
Stanford Exploration Project
6/8/2002