We can define our optimization goal as:
| |
(1) |
For this problem, we needed to apply some sort of regularization to ensure that the solution is smooth.
| |
(2) |
| |
(3) |
A computation template for the method of simulated annealing is
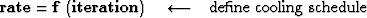
iterate {
if
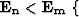
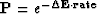
if
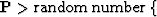
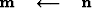
}
The model (![]() ) is a vector which defines the extracted lags from
the cross-correlagram (
) is a vector which defines the extracted lags from
the cross-correlagram (![]() ).
Energy (
).
Energy (![]() ) is what we are trying to minimize by finding the
smoothest path with the lowest energy across the cross-correlagram.
The trial model (
) is what we are trying to minimize by finding the
smoothest path with the lowest energy across the cross-correlagram.
The trial model (![]() ) is a vector the same size as
) is a vector the same size as ![]() .We define a
.We define a ![]() parameter to follow a cooling schedule as a
function of iterations.
A computation template for the method of simulated annealing is
parameter to follow a cooling schedule as a
function of iterations.
A computation template for the method of simulated annealing is ![]() ,a probability value assigned to a trial vector (
,a probability value assigned to a trial vector (![]() ).
If a random value is less than this probability value, the trial vector
will be accepted even if it has a larger energy.
This will allow the solution to escape local minima.
This is analogous to cooling magma; when the temperature is high,
it is less likely to get locked into position.
As the number of iterations increases,
).
If a random value is less than this probability value, the trial vector
will be accepted even if it has a larger energy.
This will allow the solution to escape local minima.
This is analogous to cooling magma; when the temperature is high,
it is less likely to get locked into position.
As the number of iterations increases, ![]() becomes smaller,
making it less likely to accept a solution with greater energy.
If the rate is sufficiently small, this method should converge to
the global minimum.
becomes smaller,
making it less likely to accept a solution with greater energy.
If the rate is sufficiently small, this method should converge to
the global minimum.
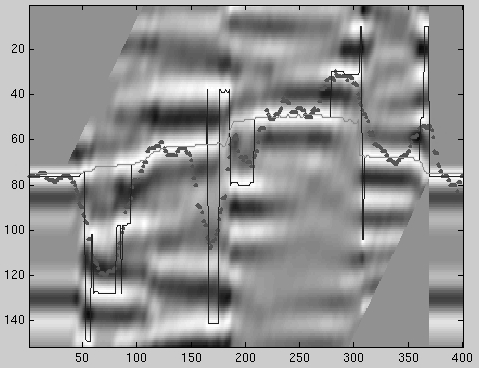
I applied this method to estimate fault slip.
The result is in Figure 9.
The dots represent the annealing solution.
The initial guess for ![]() was the maximum, the solid line.
This required numerous iterations and, although it appears that it may be
heading toward convergence (the light solid line), it may not be.
In fact, the added complication of the
was the maximum, the solid line.
This required numerous iterations and, although it appears that it may be
heading toward convergence (the light solid line), it may not be.
In fact, the added complication of the ![]() parameter makes it
quite likely to converge to a flat model.
The regularization is causing the slow convergence because randomly
changing model points tend to cause an extremely unsmooth solution.
Therefore, the regularization part is throwing out most of the
possible solutions because they are too rough.
parameter makes it
quite likely to converge to a flat model.
The regularization is causing the slow convergence because randomly
changing model points tend to cause an extremely unsmooth solution.
Therefore, the regularization part is throwing out most of the
possible solutions because they are too rough.
 |