




Next: Description of the Algorithm
Up: Theory Overview
Previous: Time-variant Filtering
The NMO correction time for the small offset-spread approximation is given
by the well-known hyperbolic equation Yilmaz (1987):
| 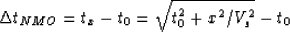 |
(8) |
where x is the trace offset, tx is the two-way travel time at offset x,
t0 is the two-way travel time at zero offset (normal incidence trace) and
Vs is the stacking velocity. Clearly, for a given trace different samples
will have different NMO correction times even if the velocity is constant.
Shallow events on the farthest trace with the slowest velocity have the maximum
NMO-correction time whereas deep events on the near traces with the fastest
velocity will have the minimum NMO-correction time. It is also important to
note that in general some fractional sample interpolation will be required
since we cannot expect the values of 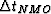 to be integer multiples
of the sampling interval.
to be integer multiples
of the sampling interval.
In order to apply the non-stationary filtering algorithm we need to
recast the NMO equation as an all-pass non-stationary filter
that will simply shift each sample by the given value of 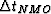 . This
can easily be achieved in the frequency domain by a linear phase shift with
slope proportional to the value of
. This
can easily be achieved in the frequency domain by a linear phase shift with
slope proportional to the value of 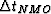 . In principle, any value
of
. In principle, any value
of 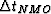 can be handled, so no fractional interpolation is
required. For the sake of efficiency, however, it is convenient to precompute
a given number of
can be handled, so no fractional interpolation is
required. For the sake of efficiency, however, it is convenient to precompute
a given number of 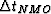 values. The accuracy of the implicit
fractional interpolation is determined by the number of precomputed
values. The accuracy of the implicit
fractional interpolation is determined by the number of precomputed
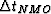 values and so can be controlled as an input parameter.
Clearly, this parameter controls the trade-off between accuracy and speed
of computation.
values and so can be controlled as an input parameter.
Clearly, this parameter controls the trade-off between accuracy and speed
of computation.





Next: Description of the Algorithm
Up: Theory Overview
Previous: Time-variant Filtering
Stanford Exploration Project
6/8/2002
![]() . This
can easily be achieved in the frequency domain by a linear phase shift with
slope proportional to the value of
. This
can easily be achieved in the frequency domain by a linear phase shift with
slope proportional to the value of ![]() . In principle, any value
of
. In principle, any value
of ![]() can be handled, so no fractional interpolation is
required. For the sake of efficiency, however, it is convenient to precompute
a given number of
can be handled, so no fractional interpolation is
required. For the sake of efficiency, however, it is convenient to precompute
a given number of ![]() values. The accuracy of the implicit
fractional interpolation is determined by the number of precomputed
values. The accuracy of the implicit
fractional interpolation is determined by the number of precomputed
![]() values and so can be controlled as an input parameter.
Clearly, this parameter controls the trade-off between accuracy and speed
of computation.
values and so can be controlled as an input parameter.
Clearly, this parameter controls the trade-off between accuracy and speed
of computation.