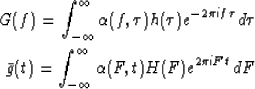Next: Forward and Inverse NMO
Up: Theory Overview
Previous: Theory Overview
In a linear time-invariant (stationary) filter
the output g(t) is related to the input h(t) by the convolution
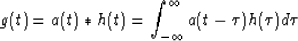
where a(t) is the impulse response of the filter. In order to extend
the applicability of this simple expression for the response of a
non-stationary filter, we could replace 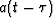 in the previous
equation with the more general expression
in the previous
equation with the more general expression 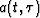 , indicating that the
impulse response itself is now a function of the input time
, indicating that the
impulse response itself is now a function of the input time  . This
expression, however, is too general and gives little insight into what
the response of such a time-variant filter would be. Margrave,
Margrave (1998) propose to
maintain the convolutional nature of the impulse response by adding an
explicit time dependence to it, that is, replacing
. This
expression, however, is too general and gives little insight into what
the response of such a time-variant filter would be. Margrave,
Margrave (1998) propose to
maintain the convolutional nature of the impulse response by adding an
explicit time dependence to it, that is, replacing 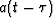 with
either
with
either 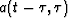 (convolution) or
(convolution) or 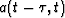 (combination). The
formal definitions of non-stationary convolution and combination are,
respectively Margrave (1998)
(combination). The
formal definitions of non-stationary convolution and combination are,
respectively Margrave (1998)
| 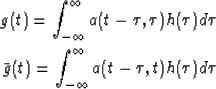 |
(1) |
| (2) |
These equations are clearly straightforward extensions of the stationary
convolution concept. The introduction of the second index accounts for
the non-stationarity. Comparing the two equations we see that the difference
between non-stationary convolution and combination lies in the way the
impulse responses are considered in the convolutional matrix. In non-stationary
convolution the filter impulse responses (as a function of input time  )correspond to the columns of the matrix, whereas in the non-stationary
convolution case they correspond (as a function of the output time t) to the
rows of the matrix (time reversed).
)correspond to the columns of the matrix, whereas in the non-stationary
convolution case they correspond (as a function of the output time t) to the
rows of the matrix (time reversed).
Just as with stationary filtering, it is convenient to find equivalent
expressions in the frequency domain. These expressions are Margrave (1998)
| 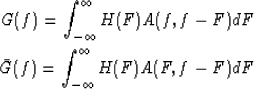 |
(3) |
| (4) |
where f and F are the Fourier duals of t and  respectively and
H(F) and G(f) are the Fourier transforms of
respectively and
H(F) and G(f) are the Fourier transforms of 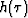 and g(t).
It is interesting to notice from these equations that non-stationary
convolution in time domain translates into non-stationary combination in the
frequency domain and vice versa. This is as opposed to the stationary case
in which convolution in time domain corresponds to multiplication in the
frequency domain.
and g(t).
It is interesting to notice from these equations that non-stationary
convolution in time domain translates into non-stationary combination in the
frequency domain and vice versa. This is as opposed to the stationary case
in which convolution in time domain corresponds to multiplication in the
frequency domain.
Since we now have two time indexes (t representing the filter
samples and  to keep track of the sample index to which each filter
is applied), it is possible
to have a third domain of computation, the so-called mixed domain in which
the impulse response of the filters in the convolutional matrix are replaced
with their corresponding frequency spectra. The equations to apply
non-stationary filtering in the mixed domain are slow generalized Fourier
transforms given by Margrave (1998)
to keep track of the sample index to which each filter
is applied), it is possible
to have a third domain of computation, the so-called mixed domain in which
the impulse response of the filters in the convolutional matrix are replaced
with their corresponding frequency spectra. The equations to apply
non-stationary filtering in the mixed domain are slow generalized Fourier
transforms given by Margrave (1998)
| 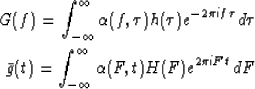 |
(5) |
| (6) |
where 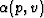 is the so-called non-stationary transfer function which
is the basic matrix in which the horizontal axis is time and the vertical axis
is frequency (an example of this matrix will be given below). The transfer
function is given by
is the so-called non-stationary transfer function which
is the basic matrix in which the horizontal axis is time and the vertical axis
is frequency (an example of this matrix will be given below). The transfer
function is given by
| 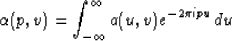 |
(7) |
where a(u,v) is the matrix of impulse responses, that is, the matrix with
 as its horizontal axis and t as its vertical axis (again, an example
will be shown below).
as its horizontal axis and t as its vertical axis (again, an example
will be shown below).





Next: Forward and Inverse NMO
Up: Theory Overview
Previous: Theory Overview
Stanford Exploration Project
6/8/2002
![]()
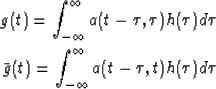
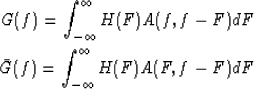
![]() to keep track of the sample index to which each filter
is applied), it is possible
to have a third domain of computation, the so-called mixed domain in which
the impulse response of the filters in the convolutional matrix are replaced
with their corresponding frequency spectra. The equations to apply
non-stationary filtering in the mixed domain are slow generalized Fourier
transforms given by Margrave (1998)
to keep track of the sample index to which each filter
is applied), it is possible
to have a third domain of computation, the so-called mixed domain in which
the impulse response of the filters in the convolutional matrix are replaced
with their corresponding frequency spectra. The equations to apply
non-stationary filtering in the mixed domain are slow generalized Fourier
transforms given by Margrave (1998)