Geometrical interpretation of PS-AMO

A trace with input offset vector $\vec{h}_1$ and midpoint position $\vec{x}$ is first transformed to its corresponding CCP position and zero offset. By defining the new offset and azimuth position and by applying inverse PS-DMO, we transform the data to a new CCP position and its corresponding CMP position.

Here, we follow the same procedure as Biondi et al. (1998); Fomel and Biondi (1995) for the derivation of the PS-AMO operator.

First, we refer to equations (1) and (2) in order to understand the relationship between CMP and CCP for the 3D case. We rewrite equation (2) as

$$\Vert \vec{y}\Vert^2 = \Vert \vec{x}\Vert^2 + \Vert \vec{D}\Vert^2 + 2 \Vert \vec{x} \Vert \Vert \vec{D} \Vert \cos\lambda,$$

where $\lambda$ is the angle between the midpoint vector ($\vec{x}$) and the transformation vector ($\vec{D}$).

We can then rewrite equation (1) as

 

$$\frac{t_0^2}{t_n^2} + \frac{\Vert\vec{x}\Vert^2}{\Vert\vec{H... ...c{x}\Vert\Vert\vec{D}\Vert\cos\lambda}{\Vert\vec{H}\Vert^2} =1.$$ (5)

$\vec{D}$ is an extension of $\vec{h}$ and lies in the CCP space. Figure 1 shows both $\vec{h}$ and $\vec{D}$ in the same plane. Since the vectors are parallel, the angle between $\vec{x}$ and $\vec{D}$ is the same as the angle between $\vec{x}$ and $\vec{h}$.If the coordinate system is aligned with the midpoint coordinates, then the angle $\lambda$ is the same as the azimuth ($\lambda=\theta$). $\lambda$ changes after and before PS-AMO. This variation is responsible for the event movement along the common conversion point.

 

rot Figure 1 Definition of offset vector 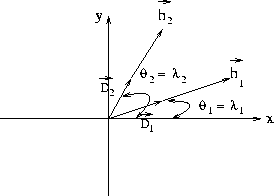$\vec{h}$ and transformation vector $\vec{D}$, before and after PS-AMO

Figure 2 shows how event movement along CCP changes with depth. This is due to the dependence of $\vec{D}$ with respect to v_p, $\gamma$ and t_n. This variance with depth will persist even in a constant velocity media. Figure 2 also illustrates that the time after PS-AMO (t₂) has a new $\vec{h}$ and $\vec{D}$, therefore, a new CCP position.

 

plane2 Figure 2 Comparison between the CMP and CCP position in the PS-AMO operator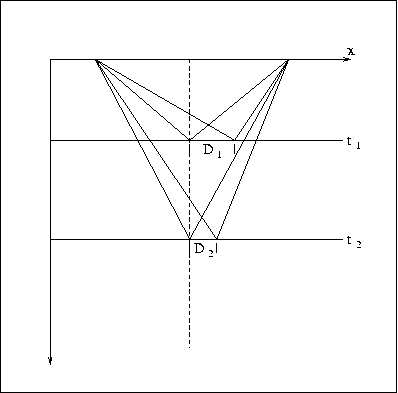

Continuing with the procedure presented by Fomel and Biondi (1995) to obtain the PS-AMO operator, we cascade PS-DMO [equation (5)] with its inverse. Figure 3 shows a scheme of the PS-AMO transformation. A trace with input offset vector $\vec{h}_1$ and midpoint at the origin is transformed into equivalent data with output offset vector $\vec{h}_2$ and midpoint position $\vec{x}$. The data is first transformed to its corresponding CCP position and $\vec{D} = \vec{0}$. Subsequently, the inverse PS-DMO repositions the data to a new midpoint position $\vec{x}$ with a new offset vector $\vec{h}_2$.

 

plane Figure 3 CMP-CCP plane, PS-AMO geometrical interpretation.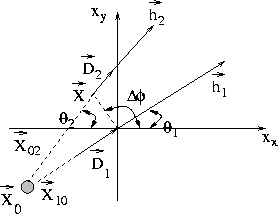

The new trace position is defined by

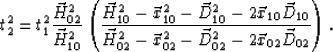$$t_2^2=t_1^2 \frac{\vec{H}_{02}^2}{\vec{H}_{10}^2}\left( \fra... ...x}_{02}^2 -\vec{D}_{02}^2 -2 \vec{x}_{02}\vec{D}_{02}} \right).$$ (6)

Both $\vec{x}_{10}$ and $\vec{x}_{02}$ can be expressed as terms of the final midpoint position $\vec{x}$ by using the rule of sines in the triangle ($\vec{x}$,$\vec{x}_{10}$,$\vec{x}_{02}$)in Figure 3 as

$$\begin{eqnarray} \vec{x}_{10} & = & \vec{x} \frac{\sin(\theta_2 - \Delta\phi)}{\... ...\sin(\theta_1 - \Delta\phi)}{\sin(\theta_1 - \theta_2)}. \nonumber\end{eqnarray}$$

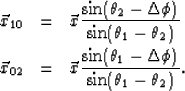The final expression takes the form of

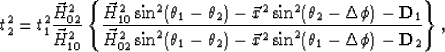$$t_2^2=t_1^2 \frac{\vec{H}_{02}^2}{\vec{H}_{10}^2}\left \{ \f... ...}^2\sin^2(\theta_1 - \Delta\phi) - \mbox{{\bf D}}_2} \right \},$$ (7)

where

$$\begin{eqnarray} \mbox{{\bf D}}_1 & = & \vec{D}_{10}^2\sin^2(\theta_1 - \theta_2... ...a_1 - \Delta\phi)\sin(\theta_1 - \theta_2) \cos\theta_2. \nonumber\end{eqnarray}$$

This expression represents the azimuth rotation in both the CCP domain and the CMP domain.