




Next: A hybrid attenuation scheme
Up: Improving adaptive subtraction
Previous: Improving adaptive subtraction
The goal of adaptive subtraction is as follows: given a time series
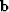 and a desired time series
and a desired time series 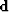 , we seek a filter
, we seek a filter
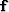 that minimizes the difference between
that minimizes the difference between 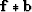 and
and
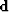 where * is convolution. We can rewrite this definition
in the fitting goal
where * is convolution. We can rewrite this definition
in the fitting goal
| 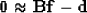 |
(1) |
where 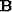 represents the convolution with the time series
represents the convolution with the time series
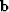 . We can minimize this fitting goal in a least-squares sense
leading to the objective function
. We can minimize this fitting goal in a least-squares sense
leading to the objective function
| 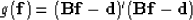 |
(2) |
where (') is the transpose. The minimum energy solution is given by
| 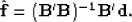 |
(3) |
where 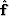 is the least-squares estimate of
is the least-squares estimate of 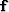 .This approach is very popular but has some intrinsic limitations.
In particular
.This approach is very popular but has some intrinsic limitations.
In particular 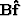 is by construction orthogonal
to the residual
is by construction orthogonal
to the residual 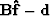 . In the multiple attenuation
problem
. In the multiple attenuation
problem 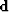 is the data,
is the data, 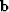 the multiple model and
the multiple model and
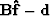 the estimated primaries. If both signal and
noise are correlated, the separation will suffer because of
the orthogonality principle.
the estimated primaries. If both signal and
noise are correlated, the separation will suffer because of
the orthogonality principle.
From now on I will refer to this method as the ``standard approach''.
In the next section I propose improving the adaptive subtraction
scheme. This improvement leads to an unbiased matched-filter
estimation when both signal and noise are correlated.





Next: A hybrid attenuation scheme
Up: Improving adaptive subtraction
Previous: Improving adaptive subtraction
Stanford Exploration Project
6/7/2002