Adjoint non-stationary convolution and combination

The adjoint of non-stationary convolution can be written as  

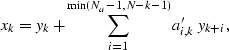$$x_k = y_k + \sum_{i=1}^{\min(N_a-1, N-k-1)} a'_{i,k} \; y_{k+i},$$ (118)

and the adjoint of non-stationary combination can be written as  

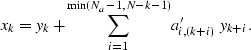$$x_k = y_k + \sum_{i=1}^{\min(N_a-1, N-k-1)} a'_{i,(k+i)} \; y_{k+i}.$$ (119)

For many applications, the adjoint of a linear operator is the same operator applied in a (conjugate) time-reversed sense. For example, causal and anti-causal filtering, integration, differentiation, upward and downward continuation, finite-difference modeling and reverse-time migration etc.

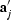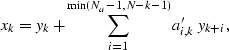
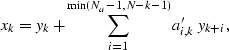
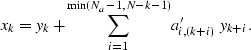
For non-stationary filtering, it is important to realize this is not the case: the adjoint of non-stationary convolution is time-reversed non-stationary combination, and vice-versa. Therefore, the output of adjoint combination is a superposition of scaled time-reversed filters, ${\bf a}'_j$. So for anti-causal non-stationary filtering, it may be advantageous to apply adjoint combination, as opposed to adjoint convolution.