




Next: Combining model-space and data-space
Up: Model versus data normalization
Previous: Computational cost
If the estimation problem, 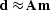 ,
is underdetermined, then a standard approach is to find the solution with
the minimum norm. For the L2 norm, this is the solution to
,
is underdetermined, then a standard approach is to find the solution with
the minimum norm. For the L2 norm, this is the solution to
| 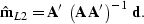 |
(98) |
As a corollary to the the methodology outlined above for creating
model-space weighting functions, Claerbout (1998a) suggests constructing
diagonal approximations to 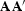 by probing the
operator with a reference data vector,
by probing the
operator with a reference data vector, 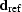 .
This gives data-space weighting functions of the form,
.
This gives data-space weighting functions of the form,
| 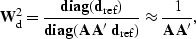 |
(99) |
which can be used to provide a direct approximation to the
solution in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ),
),
| 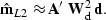 |
(100) |
Alternatively, we could use 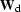 as a data-space
preconditioning operator to help speed up
the convergence of an iterative solver:
as a data-space
preconditioning operator to help speed up
the convergence of an iterative solver:
| 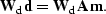 |
(101) |





Next: Combining model-space and data-space
Up: Model versus data normalization
Previous: Computational cost
Stanford Exploration Project
5/27/2001
![]() by probing the
operator with a reference data vector,
by probing the
operator with a reference data vector, ![]() .
This gives data-space weighting functions of the form,
.
This gives data-space weighting functions of the form,
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ),
),
![]() as a data-space
preconditioning operator to help speed up
the convergence of an iterative solver:
as a data-space
preconditioning operator to help speed up
the convergence of an iterative solver: