




Next: Spectral factorization of seismic
Up: Applications of multi-dimensional spectral
Previous: Spectral factorization of partial
Most industrial-strength geophysics involves filtering the recorded
data with the adjoint of the physical process that created it.
If the true earth model is 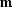 and
and 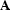 is the physical
forward modeling operator, then the image we compute is
is the physical
forward modeling operator, then the image we compute is
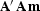 .
In the final part of this thesis, I form approximations to the
.
In the final part of this thesis, I form approximations to the
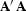 operators associated with prestack depth
migration that are diagonal in physical space.
Since the approximations are diagonal, I can easily compute two
factors simply by taking the square root of their diagonal elements.
These factors are also diagonal, and hence easily invertible.
These diagonal factors can then be applied directly to
the migrated image to produce an image whose amplitude more closely
resembles those of the true earth model.
Alternatively, the factors can be applied in concert with the original
operator, to produce a new dimensionless composite operator, which is
more easily invertible with iterative linear solvers.
operators associated with prestack depth
migration that are diagonal in physical space.
Since the approximations are diagonal, I can easily compute two
factors simply by taking the square root of their diagonal elements.
These factors are also diagonal, and hence easily invertible.
These diagonal factors can then be applied directly to
the migrated image to produce an image whose amplitude more closely
resembles those of the true earth model.
Alternatively, the factors can be applied in concert with the original
operator, to produce a new dimensionless composite operator, which is
more easily invertible with iterative linear solvers.
In Chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , I discuss how to calculate the
shot-illumination cheaply during shot-profile migration.
I then show that for sparse-shot geometries with dense receiver
coverage this weighting function can completely compensate for
illumination problems on flat events.
, I discuss how to calculate the
shot-illumination cheaply during shot-profile migration.
I then show that for sparse-shot geometries with dense receiver
coverage this weighting function can completely compensate for
illumination problems on flat events.
Lastly, in Chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , I compare alternative methods
of computing appropriate diagonal model-space and data-space weighting
functions appropriate for generic linear operators, and discuss how
model-space and data-space weights can be calculated and applied
simultaneously.
, I compare alternative methods
of computing appropriate diagonal model-space and data-space weighting
functions appropriate for generic linear operators, and discuss how
model-space and data-space weights can be calculated and applied
simultaneously.





Next: Spectral factorization of seismic
Up: Applications of multi-dimensional spectral
Previous: Spectral factorization of partial
Stanford Exploration Project
5/27/2001
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , I discuss how to calculate the
shot-illumination cheaply during shot-profile migration.
I then show that for sparse-shot geometries with dense receiver
coverage this weighting function can completely compensate for
illumination problems on flat events.
, I discuss how to calculate the
shot-illumination cheaply during shot-profile migration.
I then show that for sparse-shot geometries with dense receiver
coverage this weighting function can completely compensate for
illumination problems on flat events.