Numerical example

The SEG-EAGE salt-dome synthetic dataset provides a good test-bed for 3-D migration algorithms since it contains both complex velocity and steeply-dipping reflectors Vaillant (1999). The images in this chapter are produced by migrating a zero-offset subvolume of the full 3-D dataset.

Figure  shows a slightly smoothed version of the true SEG/EAGE velocity model, and Figure  shows the results of migrating the dataset with this model and the helical factorization of the conventional 45$^\circ$ equation Claerbout (1985). Both the top and bottom of the salt are well-imaged throughout most of the model. Unsurprisingly, however, problems exist around x=7000 m, in the area where steep canyons disrupt the top salt. The growth in amplitude of the migrated image around this area is related to a mild instability in the algorithm that I discuss in the next section.

 

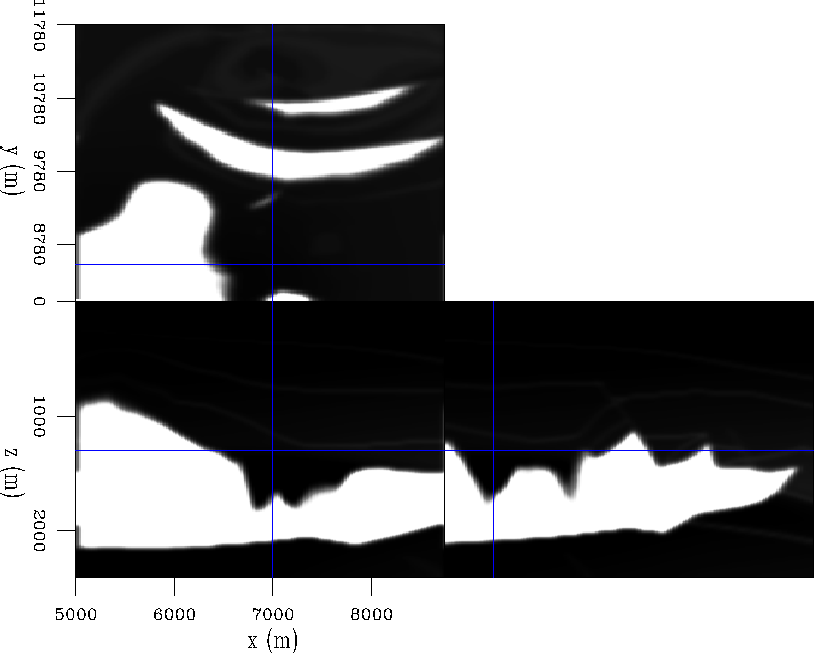
segvelunstabb
Figure 2 Velocity model with strong lateral velocity variations. Velocity varies between 1.5 km/s in the near surface sediments to 4.5 km/s in the salt.

 

segmig5
Figure 3 Result of migrating a subvolume from the zero-offset 3-D SEG/EAGE salt model with the non-stationary helical factorization.