




Next: Helical boundary conditions
Up: Implicit extrapolation theory
Previous: Implicit extrapolation theory
The diffraction term of the 45 equation Claerbout (1985) can
be rewritten as the following matrix equation, by inserting the rational
part of the implicit extrapolator (
equation Claerbout (1985) can
be rewritten as the following matrix equation, by inserting the rational
part of the implicit extrapolator (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) into
equation (
) into
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ):
):
| 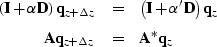 |
(38) |
| (39) |
where the complex coefficient,  can be
calculated, and
can be
calculated, and 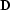 is a finite-difference representation of the
Laplacian,
is a finite-difference representation of the
Laplacian, 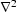 .
.
The right-hand-side of equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is known. The
challenge is to find the vector
) is known. The
challenge is to find the vector 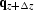 by inverting
the matrix,
by inverting
the matrix, 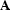 .Given the wavefield on the surface, this equation provides a way to
downward-continue in depth.
.Given the wavefield on the surface, this equation provides a way to
downward-continue in depth.
The matrices in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) represent convolution with
a scaled finite-difference Laplacian, with its main diagonal
stabilized.
In the two-dimensional problem, the
) represent convolution with
a scaled finite-difference Laplacian, with its main diagonal
stabilized.
In the two-dimensional problem, the 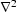 operator acts only in
the x-direction, and can be represented by the three-point
convolutional filter, d=(1,-2,1). The matrix,
operator acts only in
the x-direction, and can be represented by the three-point
convolutional filter, d=(1,-2,1). The matrix, 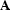 ,therefore, has a tridiagonal structure, which can be inverted
efficiently with a recursive solver.
,therefore, has a tridiagonal structure, which can be inverted
efficiently with a recursive solver.
In three-dimensional wavefield extrapolation, the 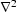 operator
acts in both the x and y-directions.
operator
acts in both the x and y-directions.
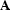 therefore represents a 2-D convolution, and
d can be represented by the a simple 5-point filter,
therefore represents a 2-D convolution, and
d can be represented by the a simple 5-point filter,
| ![\begin{displaymath}
d = \left[ \begin{array}
{ccc}
& 1 & \\ 1 & -4 & 1\\ & 1 & \end{array} \right] \end{displaymath}](img105.gif) |
(40) |
or a more isotropic 9-point filter Iserles (1996),
| ![\begin{displaymath}
d = \left[ \begin{array}
{ccc}
1/6 & 2/3 & 1/6 \\ 2/3 & -10/3 & 2/3\\ 1/6 & 2/3 & 1/6\end{array} \right]\end{displaymath}](img106.gif) |
(41) |
The vectors 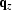 and
and 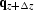 contain the
wavefield at every point in the (x,y)-plane.
Therefore, the convolution matrices that operate on
them are square with dimensions
contain the
wavefield at every point in the (x,y)-plane.
Therefore, the convolution matrices that operate on
them are square with dimensions 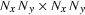 .
As an illustration, for a
.
As an illustration, for a 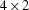 spatial plane, the structure of
matrix
spatial plane, the structure of
matrix 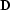 with the five-point approximation and transient
boundary conditions, will be the blocked-tridiagonal matrix
with the five-point approximation and transient
boundary conditions, will be the blocked-tridiagonal matrix
| ![\begin{displaymath}
{\bf D} = \left[
\begin{array}
{cccc\vert cccc}
-4 & 1 & . ...
... & 1 \\
. & . & . & 1 & . & . & 1 & -4 \\ \end{array}\right]\end{displaymath}](img110.gif) |
(42) |
This blocked system cannot be easily
inverted, even for the case of constant velocity, since the missing
coefficients on the second diagonals break the Toeplitz structure.





Next: Helical boundary conditions
Up: Implicit extrapolation theory
Previous: Implicit extrapolation theory
Stanford Exploration Project
5/27/2001
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) into
equation (
) into
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ):
):
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is known. The
challenge is to find the vector
) is known. The
challenge is to find the vector ![]() by inverting
the matrix,
by inverting
the matrix, ![]() .Given the wavefield on the surface, this equation provides a way to
downward-continue in depth.
.Given the wavefield on the surface, this equation provides a way to
downward-continue in depth.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) represent convolution with
a scaled finite-difference Laplacian, with its main diagonal
stabilized.
In the two-dimensional problem, the
) represent convolution with
a scaled finite-difference Laplacian, with its main diagonal
stabilized.
In the two-dimensional problem, the ![]() operator acts only in
the x-direction, and can be represented by the three-point
convolutional filter, d=(1,-2,1). The matrix,
operator acts only in
the x-direction, and can be represented by the three-point
convolutional filter, d=(1,-2,1). The matrix, ![]() ,therefore, has a tridiagonal structure, which can be inverted
efficiently with a recursive solver.
,therefore, has a tridiagonal structure, which can be inverted
efficiently with a recursive solver.
![]() operator
acts in both the x and y-directions.
operator
acts in both the x and y-directions.
![]() therefore represents a 2-D convolution, and
d can be represented by the a simple 5-point filter,
therefore represents a 2-D convolution, and
d can be represented by the a simple 5-point filter,
![\begin{displaymath}
d = \left[ \begin{array}
{ccc}
& 1 & \\ 1 & -4 & 1\\ & 1 & \end{array} \right] \end{displaymath}](img105.gif)
![\begin{displaymath}
d = \left[ \begin{array}
{ccc}
1/6 & 2/3 & 1/6 \\ 2/3 & -10/3 & 2/3\\ 1/6 & 2/3 & 1/6\end{array} \right]\end{displaymath}](img106.gif)
![\begin{displaymath}
{\bf D} = \left[
\begin{array}
{cccc\vert cccc}
-4 & 1 & . ...
... & 1 \\
. & . & . & 1 & . & . & 1 & -4 \\ \end{array}\right]\end{displaymath}](img110.gif)