




Next: Kirchhoff model and the
Up: Confirmation of offset continuation
Previous: Confirmation of offset continuation
In this subsection, I discuss the Kirchhoff approximate integral
representation of the upward propagating response to a single
reflector with separated source and receiver points. I then show how
the amplitude of this integrand is related to the zero-offset
amplitude at the source receiver point on the ray that makes equal
angles at the scattering point with the rays from the separated source
and receiver. The Kirchhoff integral representation
Bleistein (1984); Haddon and Buchen (1981) describes the wavefield scattered from a single
reflector. This representation is applicable in situations where the
high-frequency assumption is valid (the wavelength is smaller than the
characteristic dimensions of the model) and corresponds in accuracy to
the WKBJ approximation for reflected waves. The general form of the
Kirchhoff modeling integral is
| ![\begin{displaymath}
U_S(r,s, \omega) = \int_\Sigma\,R (x;r,s)\,
{\partial \over ...
...,\left[
U_I(s, x ,\omega)\,G(x,r,\omega)\right]\,
d\Sigma \; ,\end{displaymath}](img354.gif) |
(199) |
where s and r stand for the source and the receiver locations; x
denotes a point on the reflector surface  ; R is the
reflection coefficient at
; R is the
reflection coefficient at  ; n is the upward normal to the
reflector at the point x; and UI and G are the incident
wavefield and Green's function, respectively represented by their WKBJ
approximation,
; n is the upward normal to the
reflector at the point x; and UI and G are the incident
wavefield and Green's function, respectively represented by their WKBJ
approximation,
| 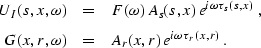 |
(200) |
| (201) |
In this equation, 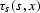 and As(s,x) are the traveltime and
the amplitude of the wave propagating from s to x;
and As(s,x) are the traveltime and
the amplitude of the wave propagating from s to x; 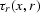 and Ar(x,r) are the corresponding quantities for the wave
propagating from x to r;
and Ar(x,r) are the corresponding quantities for the wave
propagating from x to r; 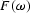 is the spectrum of the
input signal, assumed to be the transform of a band-limited impulsive
source. In the time domain, the Kirchhoff modeling integral
transforms to
is the spectrum of the
input signal, assumed to be the transform of a band-limited impulsive
source. In the time domain, the Kirchhoff modeling integral
transforms to
| ![\begin{displaymath}
u_S(r,s,t) =
\int_\Sigma\,R (x;r,s)\,{\partial \over {\part...
...r)\,
f\left(t- \tau_s(s,x) - \tau_r(x,r)\right)\right]\,
d x\;,\end{displaymath}](img360.gif) |
(202) |
with f denoting the inverse temporal transform of F. The
reflection traveltime 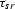 corresponds physically to the
diffraction from a point diffractor located at the point x on the
surface
corresponds physically to the
diffraction from a point diffractor located at the point x on the
surface 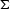 , and the amplitudes As and Ar are point
diffractor amplitudes.
, and the amplitudes As and Ar are point
diffractor amplitudes.
The main goal of this section is to test the compliance of
representation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) with the offset continuation differential
equation. The OC equation contains the derivatives of the wavefield
with respect to the parameters of observation (s, r, and
t). According to the rules of classic calculus, these derivatives
can be taken under the sign of integration in formula
(
) with the offset continuation differential
equation. The OC equation contains the derivatives of the wavefield
with respect to the parameters of observation (s, r, and
t). According to the rules of classic calculus, these derivatives
can be taken under the sign of integration in formula
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). Furthermore, since we do not assume that the true-amplitude
OC operator affects the reflection coefficient R, the
offset-dependence of this coefficient is outside the scope of
consideration. Therefore, the only term to be considered as a trial
solution to the OC equation is the kernel of the Kirchhoff integral,
which is contained in the square brackets in equations (
). Furthermore, since we do not assume that the true-amplitude
OC operator affects the reflection coefficient R, the
offset-dependence of this coefficient is outside the scope of
consideration. Therefore, the only term to be considered as a trial
solution to the OC equation is the kernel of the Kirchhoff integral,
which is contained in the square brackets in equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and
(
) and
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and has the form
) and has the form
| 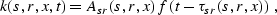 |
(203) |
where
| 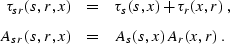 |
(204) |
| (205) |
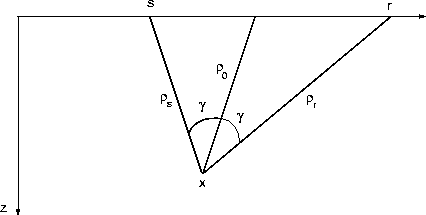
In a 3-D medium with a constant velocity v, the traveltimes and
amplitudes have the simple explicit expressions
|  |
(206) |
| (207) |
where 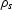 and
and 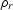 are the lengths of the incident and reflected
rays, respectively (Figure
are the lengths of the incident and reflected
rays, respectively (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). If the reflector surface
). If the reflector surface
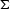 is explicitly defined by some function z=z(x), then
is explicitly defined by some function z=z(x), then
| 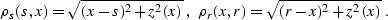 |
(208) |
cwpgen
Figure 6 Geometry of diffraction
in a constant-velocity medium: view in the reflection plane.

I then introduce a particular zero-offset amplitude, namely the
amplitude along the zero offset ray that bisects the angle between the
incident and reflected ray in this plane, as shown in Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Let us denote the square of this amplitude by
A0. That is,
. Let us denote the square of this amplitude by
A0. That is,
| 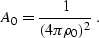 |
(209) |
As follows from equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
and (
)
and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -
-![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), the amplitude transformation in
DMO (continuation to zero offset) is characterized by the
dimensionless ratio
), the amplitude transformation in
DMO (continuation to zero offset) is characterized by the
dimensionless ratio
| 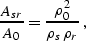 |
(210) |
where 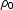 is the length of the zero-offset ray (Figure
is the length of the zero-offset ray (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).
As follows from the law of cosines,
| 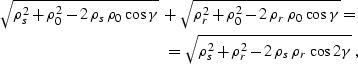 |
|
| (211) |
where 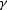 is the reflection angle, as shown in the figure.
After straightforward
algebraic transformations of equation (
is the reflection angle, as shown in the figure.
After straightforward
algebraic transformations of equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), we arrive at the
explicit relationship between the ray lengths:
), we arrive at the
explicit relationship between the ray lengths:
| 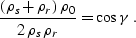 |
(212) |
Substituting (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) into (
) into (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) yields
) yields
| 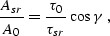 |
(213) |
where 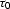 is the zero-offset two-way
traveltime (
is the zero-offset two-way
traveltime (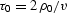 ).
).
What we have done is rewrite the finite-offset amplitude in the
Kirchhoff integral in terms of a particular zero-offset amplitude.
That zero-offset amplitude would arise as the geometric spreading
effect if there were a reflector whose dip was such that the
finite-offset pair would be specular at the scattering point. Of
course, the zero-offset ray would also be specular in this case.





Next: Kirchhoff model and the
Up: Confirmation of offset continuation
Previous: Confirmation of offset continuation
Stanford Exploration Project
12/28/2000
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) with the offset continuation differential
equation. The OC equation contains the derivatives of the wavefield
with respect to the parameters of observation (s, r, and
t). According to the rules of classic calculus, these derivatives
can be taken under the sign of integration in formula
(
) with the offset continuation differential
equation. The OC equation contains the derivatives of the wavefield
with respect to the parameters of observation (s, r, and
t). According to the rules of classic calculus, these derivatives
can be taken under the sign of integration in formula
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). Furthermore, since we do not assume that the true-amplitude
OC operator affects the reflection coefficient R, the
offset-dependence of this coefficient is outside the scope of
consideration. Therefore, the only term to be considered as a trial
solution to the OC equation is the kernel of the Kirchhoff integral,
which is contained in the square brackets in equations (
). Furthermore, since we do not assume that the true-amplitude
OC operator affects the reflection coefficient R, the
offset-dependence of this coefficient is outside the scope of
consideration. Therefore, the only term to be considered as a trial
solution to the OC equation is the kernel of the Kirchhoff integral,
which is contained in the square brackets in equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and
(
) and
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and has the form
) and has the form

![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). If the reflector surface
). If the reflector surface
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Let us denote the square of this amplitude by
A0. That is,
. Let us denote the square of this amplitude by
A0. That is,
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
and (
)
and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -
-![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), the amplitude transformation in
DMO (continuation to zero offset) is characterized by the
dimensionless ratio
), the amplitude transformation in
DMO (continuation to zero offset) is characterized by the
dimensionless ratio
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).
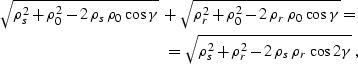
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), we arrive at the
explicit relationship between the ray lengths:
), we arrive at the
explicit relationship between the ray lengths:
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) into (
) into (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) yields
) yields