




Next: Slope estimation
Up: Regularizing local plane waves
Previous: Regularizing local plane waves
Following the physical model of local plane waves, we can define the
mathematical basis of the plane-wave destructor filters as the local
plane differential equation
| 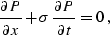 |
(98) |
where P(t,x) is the wave field, and  is the local slope, which may
also depend on t and x. In the case of a constant slope,
equation (
is the local slope, which may
also depend on t and x. In the case of a constant slope,
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) has the simple general solution
) has the simple general solution
| 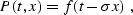 |
(99) |
where f(t) is an arbitrary waveform. Equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is
nothing more than a mathematical description of a plane wave.
) is
nothing more than a mathematical description of a plane wave.
If the slope  does not depend on t, we can transform
equation (
does not depend on t, we can transform
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) to the frequency domain, where it takes the
form of the ordinary differential equation
) to the frequency domain, where it takes the
form of the ordinary differential equation
| 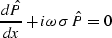 |
(100) |
and has the general solution
| 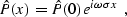 |
(101) |
where 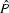 is the Fourier transform of P. The complex
exponential term in equation (
is the Fourier transform of P. The complex
exponential term in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) simply represents a shift
of a t-trace according to the slope
) simply represents a shift
of a t-trace according to the slope  and the trace separation
x.
and the trace separation
x.
In the frequency domain, the operator for transforming the trace
at position x-1 to the neighboring trace at position x is a
multiplication by 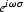 . In other words, a plane wave
can be perfectly predicted by a two-term prediction-error filter in
the F-X domain:
. In other words, a plane wave
can be perfectly predicted by a two-term prediction-error filter in
the F-X domain:
| 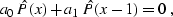 |
(102) |
where a0 = 1 and 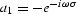 . The goal of
predicting several plane waves can be accomplished by cascading
several two-term filters. In fact, any F-X prediction-error
filter represented in the Z-transform notation as
. The goal of
predicting several plane waves can be accomplished by cascading
several two-term filters. In fact, any F-X prediction-error
filter represented in the Z-transform notation as
| 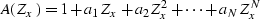 |
(103) |
can be factored into a product of two-term filters:
| 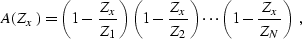 |
(104) |
where 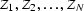 are the zeroes of
polynomial (
are the zeroes of
polynomial (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). According to equation (
). According to equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ),
the phase of each zero corresponds to the slope of a local plane wave
multiplied by the frequency. Zeroes that are not on the unit circle
carry an additional amplitude gain not included in
equation (
),
the phase of each zero corresponds to the slope of a local plane wave
multiplied by the frequency. Zeroes that are not on the unit circle
carry an additional amplitude gain not included in
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).
In order to incorporate time-varying slopes, we need to return to
the time domain and look for an appropriate analog of the phase-shift
operator (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and the plane-prediction
filter (
) and the plane-prediction
filter (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). An important property of plane-wave
propagation across different traces is that the total energy of the
transmitted wave stays invariant throughout the process. This property
is assured in the frequency-domain solution (
). An important property of plane-wave
propagation across different traces is that the total energy of the
transmitted wave stays invariant throughout the process. This property
is assured in the frequency-domain solution (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) by the fact
that the spectrum of the complex exponential
) by the fact
that the spectrum of the complex exponential 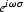 is
equal to one. In the time domain, we can reach an equivalent effect
by using an all-pass digital filter. In the Z-transform notation,
convolution with an all-pass filter takes the form
is
equal to one. In the time domain, we can reach an equivalent effect
by using an all-pass digital filter. In the Z-transform notation,
convolution with an all-pass filter takes the form
| 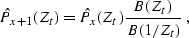 |
(105) |
where 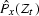 denotes the Z-transform of the corresponding
trace, and the ratio B(Zt)/B(1/Zt) is an all-pass digital filter
approximating the time-shift operator (
denotes the Z-transform of the corresponding
trace, and the ratio B(Zt)/B(1/Zt) is an all-pass digital filter
approximating the time-shift operator (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). In
finite-difference terms, equation (
). In
finite-difference terms, equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) represents an
implicit finite-difference scheme for solving equation (
) represents an
implicit finite-difference scheme for solving equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
with the initial conditions at a constant x. The coefficients of
filter B(Zt) can be determined, for example, by fitting the filter
frequency response at small frequencies to the response of the
phase-shift operator. The Taylor series technique (equating the
coefficients of the Taylor series expansion around zero frequency)
yields the expression
)
with the initial conditions at a constant x. The coefficients of
filter B(Zt) can be determined, for example, by fitting the filter
frequency response at small frequencies to the response of the
phase-shift operator. The Taylor series technique (equating the
coefficients of the Taylor series expansion around zero frequency)
yields the expression
| 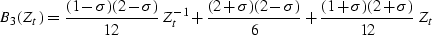 |
(106) |
for a three-point centered filter B3(Zt) and the expression
| 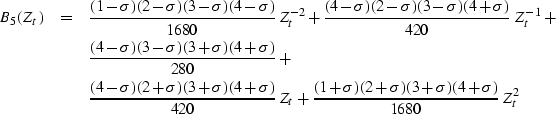 |
|
| |
| (107) |
for a five-point centered filter B5(Zt). It is easy to generalize
these expressions to longer filters.
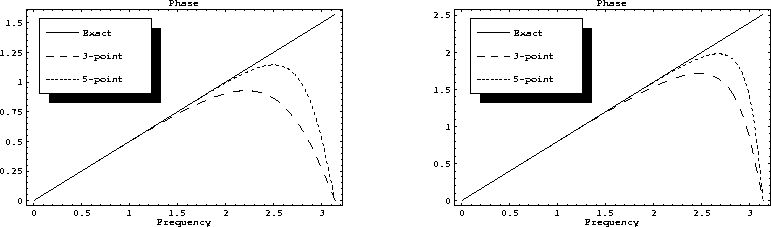
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the
phase of the all-pass filters B3(Zt)/B3(1/Zt) and
B5(Zt)/B5(1/Zt) for two values of the slope
shows the
phase of the all-pass filters B3(Zt)/B3(1/Zt) and
B5(Zt)/B5(1/Zt) for two values of the slope  in
comparison with the exact linear function of equation (
in
comparison with the exact linear function of equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
As expected, the phases match the exact line at low frequencies, and
the accuracy of the approximation increases with the length of the
filter.
phase
).
As expected, the phases match the exact line at low frequencies, and
the accuracy of the approximation increases with the length of the
filter.
phase
Figure 9 Phase of the implicit
finite-difference shift operators in comparison with the exact
solution. The left plot corresponds to 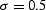 , the right plot
to
, the right plot
to 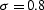 .
.





In two dimensions, equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) transforms to the
prediction equation analogous to (
) transforms to the
prediction equation analogous to (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) with the 2-D
prediction filter
) with the 2-D
prediction filter
| 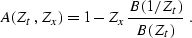 |
(108) |
In order to characterize several plane waves, we can cascade several
filters of the form (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) in a manner similar to that of
equation (
) in a manner similar to that of
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). In the examples of this chapter, I use a
modified version of the filter A(Zt,Zx), namely the filter
). In the examples of this chapter, I use a
modified version of the filter A(Zt,Zx), namely the filter
| 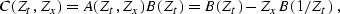 |
(109) |
which avoids the need for polynomial division. In case of the 3-point
filter (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), the 2-D filter (
), the 2-D filter (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) has exactly
six coefficients, with the second t column being a reversed copy of
the first column. When filter (
) has exactly
six coefficients, with the second t column being a reversed copy of
the first column. When filter (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is used in data
regularization problems, it can occasionally cause undesired
high-frequency oscillations in the solution, resulting from the
near-Nyquist zeroes of the polynomial B(Zt). The oscillations are
easily removed in practice with appropriate low-pass filtering.
) is used in data
regularization problems, it can occasionally cause undesired
high-frequency oscillations in the solution, resulting from the
near-Nyquist zeroes of the polynomial B(Zt). The oscillations are
easily removed in practice with appropriate low-pass filtering.
In the next subsection, I address the problem of estimating the local
slope  with filters having form (
with filters having form (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). Estimating
the slope is a necessary step for applying the finite-difference
plane-wave filters on real data.
). Estimating
the slope is a necessary step for applying the finite-difference
plane-wave filters on real data.





Next: Slope estimation
Up: Regularizing local plane waves
Previous: Regularizing local plane waves
Stanford Exploration Project
12/28/2000
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) has the simple general solution
) has the simple general solution
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is
nothing more than a mathematical description of a plane wave.
) is
nothing more than a mathematical description of a plane wave.
![]() does not depend on t, we can transform
equation (
does not depend on t, we can transform
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) to the frequency domain, where it takes the
form of the ordinary differential equation
) to the frequency domain, where it takes the
form of the ordinary differential equation
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) simply represents a shift
of a t-trace according to the slope
) simply represents a shift
of a t-trace according to the slope ![]() . In other words, a plane wave
can be perfectly predicted by a two-term prediction-error filter in
the F-X domain:
. In other words, a plane wave
can be perfectly predicted by a two-term prediction-error filter in
the F-X domain:
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). According to equation (
). According to equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ),
the phase of each zero corresponds to the slope of a local plane wave
multiplied by the frequency. Zeroes that are not on the unit circle
carry an additional amplitude gain not included in
equation (
),
the phase of each zero corresponds to the slope of a local plane wave
multiplied by the frequency. Zeroes that are not on the unit circle
carry an additional amplitude gain not included in
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and the plane-prediction
filter (
) and the plane-prediction
filter (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). An important property of plane-wave
propagation across different traces is that the total energy of the
transmitted wave stays invariant throughout the process. This property
is assured in the frequency-domain solution (
). An important property of plane-wave
propagation across different traces is that the total energy of the
transmitted wave stays invariant throughout the process. This property
is assured in the frequency-domain solution (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) by the fact
that the spectrum of the complex exponential
) by the fact
that the spectrum of the complex exponential ![]() is
equal to one. In the time domain, we can reach an equivalent effect
by using an all-pass digital filter. In the Z-transform notation,
convolution with an all-pass filter takes the form
is
equal to one. In the time domain, we can reach an equivalent effect
by using an all-pass digital filter. In the Z-transform notation,
convolution with an all-pass filter takes the form
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). In
finite-difference terms, equation (
). In
finite-difference terms, equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) represents an
implicit finite-difference scheme for solving equation (
) represents an
implicit finite-difference scheme for solving equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
with the initial conditions at a constant x. The coefficients of
filter B(Zt) can be determined, for example, by fitting the filter
frequency response at small frequencies to the response of the
phase-shift operator. The Taylor series technique (equating the
coefficients of the Taylor series expansion around zero frequency)
yields the expression
)
with the initial conditions at a constant x. The coefficients of
filter B(Zt) can be determined, for example, by fitting the filter
frequency response at small frequencies to the response of the
phase-shift operator. The Taylor series technique (equating the
coefficients of the Taylor series expansion around zero frequency)
yields the expression
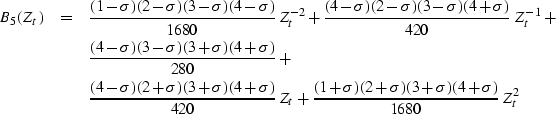
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the
phase of the all-pass filters B3(Zt)/B3(1/Zt) and
B5(Zt)/B5(1/Zt) for two values of the slope
shows the
phase of the all-pass filters B3(Zt)/B3(1/Zt) and
B5(Zt)/B5(1/Zt) for two values of the slope ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
As expected, the phases match the exact line at low frequencies, and
the accuracy of the approximation increases with the length of the
filter.
).
As expected, the phases match the exact line at low frequencies, and
the accuracy of the approximation increases with the length of the
filter.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) transforms to the
prediction equation analogous to (
) transforms to the
prediction equation analogous to (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) with the 2-D
prediction filter
) with the 2-D
prediction filter
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) in a manner similar to that of
equation (
) in a manner similar to that of
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). In the examples of this chapter, I use a
modified version of the filter A(Zt,Zx), namely the filter
). In the examples of this chapter, I use a
modified version of the filter A(Zt,Zx), namely the filter
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), the 2-D filter (
), the 2-D filter (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) has exactly
six coefficients, with the second t column being a reversed copy of
the first column. When filter (
) has exactly
six coefficients, with the second t column being a reversed copy of
the first column. When filter (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is used in data
regularization problems, it can occasionally cause undesired
high-frequency oscillations in the solution, resulting from the
near-Nyquist zeroes of the polynomial B(Zt). The oscillations are
easily removed in practice with appropriate low-pass filtering.
) is used in data
regularization problems, it can occasionally cause undesired
high-frequency oscillations in the solution, resulting from the
near-Nyquist zeroes of the polynomial B(Zt). The oscillations are
easily removed in practice with appropriate low-pass filtering.
![]() with filters having form (
with filters having form (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). Estimating
the slope is a necessary step for applying the finite-difference
plane-wave filters on real data.
). Estimating
the slope is a necessary step for applying the finite-difference
plane-wave filters on real data.