Comparison of Wilson-Burg and Kolmogoroff methods

The Kolmogoroff algorithm of spectral factorization Claerbout (1976); Kolmogoroff (1939) is widely used because of its computationally efficiency. While this method is easily extended to the multi-dimensional case with the help of helical transform Rickett and Claerbout (1999a,b), there are several circumstances that make the Wilson-Burg method more attractive in multi-dimensional filtering applications.

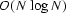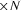• The Kolmogoroff method takes $O(N \log N)$ operations, where N is the length of the auto-correlation function. The cost of the Wilson-Burg method is proportional to the [number of iterations] $\times$ [filter length] $\times N$. If we keep the filter small and limit the number of iterations, the Wilson-Burg method can be cheaper (linear in N).
• The Kolmogoroff method works in the frequency domain and assumes periodic boundary conditions. Auto-correlation functions, therefore, need to be padded with zeros before they are Fourier transformed. For functions with zeros near the unit circle, the padding may need to be many orders of magnitude greater than the original filter length, N Rickett and Claerbout (1998). The Wilson-Burg method is implemented in the time-domain, so no padding is required.
• Newton's method (the basis of the Wilson-Burg algorithm) converges quickly when the initial guess is close to the solution. If we take advantage of this property, the method may converge in one or two iterations, reducing the cost even further. It is impossible to make use of an initial guess with the Kolmogoroff method.
• The Kolmogoroff method, when applied to helix filtering, involves the dangerous step of truncating the filter coefficients to reduce the size of the filter. If the auto-correlation function has roots close to the unit circle, truncating filter coefficients may easily lead to non-minimum-phase filters. With Wilson-Burg, we can fix the shape of the filter from the very beginning. This does not guarantee that we will find the exact solution, but at least we can obtain a reasonable minimum-phase approximation to the desired filter. The safest practical strategy in the case of an unknown initial estimate is to start with finding the longest possible filter, remove those of its coefficients that are smaller a certain threshold, and repeat the factoring process again with the shorter filter.