Decon comparisons between Burg and conjugate-gradient methods

Precision and Accuracy

Focusing on precision we arrange our study so end effects are minimal and the stationarity assumption is not stressed. We are not attempting an exhibition of known theoretical differences, but we do intend to obtain for practical work, guidelines for dealing with poorly understood numerical-analysis issues.

Reflection data is not stationary; and it comes exhibiting diverse aspects [reference Yilmaz and Cumro shot profiles]. We chose simply to test with several of our current data sets of interest. Results with three of them are included here. To simulate stationarity, Kjartansson t-squared gain is applied. We also taper the ends of the trace to avoid any transients there. Additionally, we average spectra of hundreds to thousands of traces in each data set. This average spectrum is used to devise a single decon filter applied to every trace in the data set.

We were not aware of precision issues with the Burg method, neither were we aware that it has been tested under modern environments where high order filters are easily computed.

The conjugate-direction method in GEE has some issues likewise never investigated. Theoretically it converges in a number of steps equal the filter length, but this says nothing about precision. It is easy enough to do more iterations than required. Thus we have compared the theoretical number of iterations with triple that number. Accuracy greater still should be obtainable by an additional measure that we did not try. The algorithm proceeds by updating a residual. These updates might accumulate errors. Thus, the residual could be recomputed from time-to-time during iteration. The textbook program Pef in GEE is not doing that. We could have tested that additional grasp for precision, but we did not.

More fundamentally, the Burg method builds in the stationarity assumption and minimum phase (by assuring a sequence of reflection coefficients is bounded between 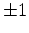$\pm 1$ ). The Pef code (concerned with multidimensional data containing gaps) makes no such effort. It could predict a growing function which is obviously non-stationary. Does that mean the output of Pef could be non-white? Likely so, but we don't know if that is a practical issue.

Decon comparisons between Burg and conjugate-gradient methods