|
|
|
|
Computational analysis of extended full waveform inversion |
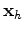 is subsurface offset and
is subsurface offset and 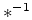 denotes a deconvolution operator over subsurface offset. This extended wave equation convolves each time slice by all subsurface offsets of velocity. The cost of extended forward modeling becomes:
denotes a deconvolution operator over subsurface offset. This extended wave equation convolves each time slice by all subsurface offsets of velocity. The cost of extended forward modeling becomes:
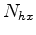 and
and 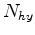 are number of subsurface offsets along the
are number of subsurface offsets along the 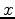 and
and 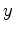 axes, respectively. By linearizing equation 7 over the velocity squared, we can compute the adjoint as:
axes, respectively. By linearizing equation 7 over the velocity squared, we can compute the adjoint as:
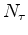 is the number of time lags. The computational disadvantage is that several time slices need to be held in memory for each time instead of the conventional two slices.
is the number of time lags. The computational disadvantage is that several time slices need to be held in memory for each time instead of the conventional two slices.
|
|
|
|
Computational analysis of extended full waveform inversion |