Next: HORIZONTAL REFLECTOR IN A
Up: Fomel & Grechka: Nonhyperbolic
Previous: Introduction
In a transversely isotropic medium, velocities of seismic waves depend
on the direction of propagation measured from the symmetry
axis. Thomsen 1986 has introduced a convenient
parametrization of this dependence, replacing the general notation of
elastic anisotropy in terms of stiffness coefficients
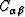 by P- and S-wave velocities along the symmetry
axis and three dimensionless parameters. As shown by Tsvankin
1996, the P-wave seismic signatures in vertically transverse
isotropic (VTI) media can be conveniently expressed in terms of
Thomsen's parameters
by P- and S-wave velocities along the symmetry
axis and three dimensionless parameters. As shown by Tsvankin
1996, the P-wave seismic signatures in vertically transverse
isotropic (VTI) media can be conveniently expressed in terms of
Thomsen's parameters  ,
, 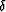 , and
, and 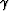 . A deviation
of these paramers from zero characterizes the relative strength of
anisotropy. Therefore, the weak anisotropy approximation
Thomsen (1986); Tsvankin and Thomsen (1994) reduces to simple
linearization.
. A deviation
of these paramers from zero characterizes the relative strength of
anisotropy. Therefore, the weak anisotropy approximation
Thomsen (1986); Tsvankin and Thomsen (1994) reduces to simple
linearization.
In weakly anisotropic VTI media, the squared group velocity Vg2 of
seismic P-waves can be expressed as a function of the group angle
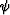 as follows:
as follows:
| 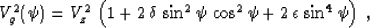 |
(1) |
where Vz = Vg(0) is the vertical velocity, and 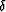 and
and
 are Thomsen's dimensionless anisotropic parameters, which
are assumed to be small quantities:
are Thomsen's dimensionless anisotropic parameters, which
are assumed to be small quantities:
| 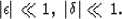 |
(2) |
Both parameters are equal to zero in the isotropic case. Their
connection with the stiffness coefficients has the following
expressions Thomsen (1986):
| 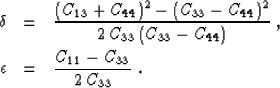 |
(3) |
| (4) |
Equation (1) is accurate up to the second-order terms in
 and
and 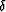 . We retain this level of accuracy throughout
this paper without additional clarification. As follows from equation
(1), the horizontal velocity Vx corresponding to the
horizontal ray propagation is
. We retain this level of accuracy throughout
this paper without additional clarification. As follows from equation
(1), the horizontal velocity Vx corresponding to the
horizontal ray propagation is
| 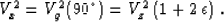 |
(5) |
Equation (5) coincides with the exact expression, which is valid
for any strength of anisotropy. Another important quantity is the
normal moveout (NMO) velocity for homogeneous VTI media with a
horizontal reflector. Its exact expression is Thomsen (1986)
| 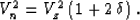 |
(6) |
One example of a physical anisotropic model is ANNIE, proposed by
Shoenberg, Muir, and Sayers 1996 to describe anisotropy
of shales. According to this model, the elasticity tensor (stiffness
matrix) in transversely isotropic shales is represented by the three
parameter approximation
| ![\begin{displaymath}
C = \left[\begin{array}
{cccccc}
\lambda + 2\,\mu_H & \lambd...
... 0 & \mu & 0 \ 0 & 0 & 0 & 0 & 0 & \mu_H \end{array}\right]\;,\end{displaymath}](img11.gif) |
(7) |
where 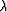 ,
, 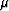 , and
, and 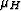 are density-normalized elastic
parameters. Formula (3) shows that Thomsen's parameter
are density-normalized elastic
parameters. Formula (3) shows that Thomsen's parameter
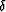 in this case is equal to zero, which corresponds to the known
fact that the normal moveout velocity for shales is approximately
equal to the vertical velocity. The parameter
in this case is equal to zero, which corresponds to the known
fact that the normal moveout velocity for shales is approximately
equal to the vertical velocity. The parameter  in this case
is defined by the equation
in this case
is defined by the equation
| 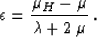 |
(8) |
It is convenient to rewrite equation (1) in the form
| 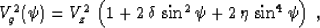 |
(9) |
where
| 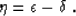 |
(10) |
The paramter  is equivalent under the weak anisotropy assumption
to the anelliptic parameter introduced by Alkhalifah and
Tsvankin 1995. For the elliptic anisotropy model,
is equivalent under the weak anisotropy assumption
to the anelliptic parameter introduced by Alkhalifah and
Tsvankin 1995. For the elliptic anisotropy model,
 equals
equals 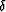 , and
, and  is equal to zero. To see why
the group velocity function becomes elliptic in this case, note that
for small
is equal to zero. To see why
the group velocity function becomes elliptic in this case, note that
for small 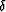 ,
,
| 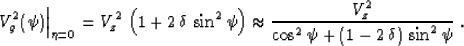 |
(11) |
In practical cases of VTI media,  is often greater than
is often greater than
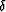 , so the anelliptic parameter
, so the anelliptic parameter  is positive.
is positive.
Another equivalent form of equation (1) follows from a
substitution of the three characteristic velocities Vz, Vx, and
Vn, as follows:
| 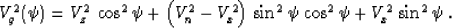 |
(12) |
It is apparent in formula (12) that, in the linear
approximation, the anelliptic behavior of anisotropy is controlled by
the difference between the normal moveout and horizontal velocities.
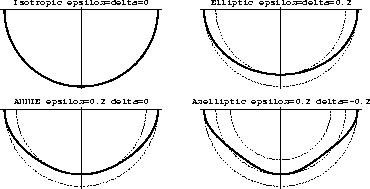
We illustrate different types of anisotropy in Figure 1,
which shows the wavefronts for different values of the anisotropic
parameters. The wavefront, circular in the isotropic case
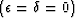 , appears elliptic if
, appears elliptic if 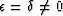 . If
. If
 is greater than zero, and
is greater than zero, and 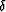 is smaller than zero,
the three characteristic velocities satisfy the inequality Vx > Vz
> Vn.
is smaller than zero,
the three characteristic velocities satisfy the inequality Vx > Vz
> Vn.
nmofro
Figure 1 Wavefronts in weakly
anisotropic media. Solid curves denote anisotropic wavefronts. Dashed
curves denote isotropic wavefronts for the corresponding vertical,
horizontal, and normal moveout velocities. Top left: isotropic case
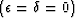 ; top right: elliptic case
; top right: elliptic case
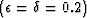 ; bottom left: ANNIE model
; bottom left: ANNIE model 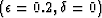 ; bottom right: strongly anelliptic case
; bottom right: strongly anelliptic case 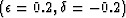 .
.










Next: HORIZONTAL REFLECTOR IN A
Up: Fomel & Grechka: Nonhyperbolic
Previous: Introduction
Stanford Exploration Project
9/12/2000
![]() as follows:
as follows:
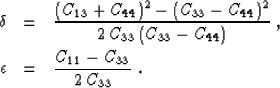
![]() and
and ![]() . We retain this level of accuracy throughout
this paper without additional clarification. As follows from equation
(1), the horizontal velocity Vx corresponding to the
horizontal ray propagation is
. We retain this level of accuracy throughout
this paper without additional clarification. As follows from equation
(1), the horizontal velocity Vx corresponding to the
horizontal ray propagation is
![\begin{displaymath}
C = \left[\begin{array}
{cccccc}
\lambda + 2\,\mu_H & \lambd...
... 0 & \mu & 0 \ 0 & 0 & 0 & 0 & 0 & \mu_H \end{array}\right]\;,\end{displaymath}](img11.gif)
![]() , appears elliptic if
, appears elliptic if ![]() . If
. If
![]() is greater than zero, and
is greater than zero, and ![]() is smaller than zero,
the three characteristic velocities satisfy the inequality Vx > Vz
> Vn.
is smaller than zero,
the three characteristic velocities satisfy the inequality Vx > Vz
> Vn.