Now for the paradox.
Imagine ![]() in Figure 8.
Will we see the same limit as results from the ensemble average?
Here are two contradictory points of view:
in Figure 8.
Will we see the same limit as results from the ensemble average?
Here are two contradictory points of view:
To examine this issue further,
let us discover how these autocorrelations decrease
to zero with n (the number of samples).
Figure 9 shows the autocorrelation samples as a function of n
in steps of n increasing by factors of four.
Thus ![]() increases by factors of two.
increases by factors of two.
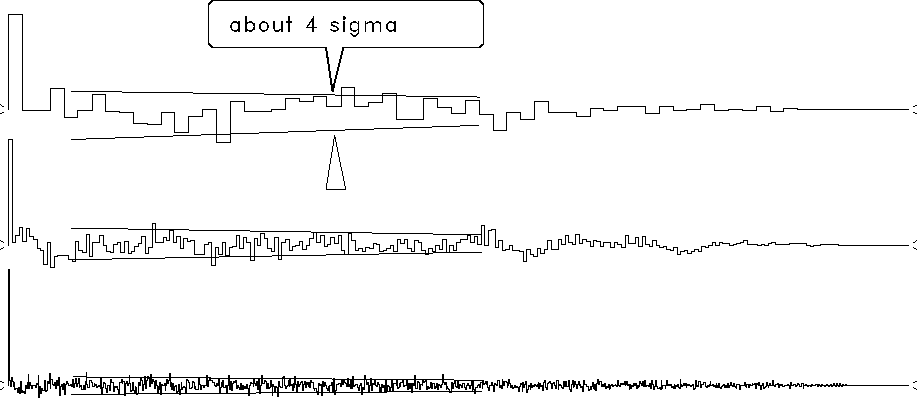 |
Each autocorrelation in the figure was normalized at zero lag.
We see the sample variance for nonzero lags of the autocorrelation
dropping off as ![]() .We also observe that the ratios between the values for the first nonzero
lags and the value at lag zero roughly fit
.We also observe that the ratios between the values for the first nonzero
lags and the value at lag zero roughly fit ![]() .Notice also that the fluctuations drop off with lag.
The drop-off goes to zero at a lag equal to the sample length,
because the number of terms in the autocorrelation
diminishes to zero at that lag.
A first impression is that the autocorrelation fits a triangular envelope.
More careful inspection, however, shows
that the triangle bulges upward at wide offsets,
or large values of k
(this is slightly clearer in Figure 8).
Each of these observations has an analytic explanation found in PVI.
.Notice also that the fluctuations drop off with lag.
The drop-off goes to zero at a lag equal to the sample length,
because the number of terms in the autocorrelation
diminishes to zero at that lag.
A first impression is that the autocorrelation fits a triangular envelope.
More careful inspection, however, shows
that the triangle bulges upward at wide offsets,
or large values of k
(this is slightly clearer in Figure 8).
Each of these observations has an analytic explanation found in PVI.