|
leakend
Figure 6 Pulses at various distances from a side boundary smoothed with two-sided leaky integration and zero-slope side conditions. Beyond the last value at the edge is a theoretical value that is the same as the edge value. | 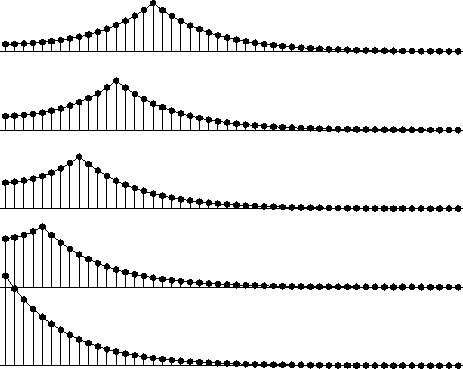 |
The two-sided leaky integral commonly arises as an even function, which is an ordinary leaky integral in one direction followed by another in the opposite direction. We will see also that the single leaky integral need not be causal; it could be an odd function.
The causal-integration operator flows one direction in time. Anticausal integration flows the other. Causal integration followed by anticausal integration makes a symmetrical smoothing operation, frequently used on the horizontal space axis. Since the idea of integration is generally associated with a long decay constant, and since data is generally limited in space, particular attention is usually given to the side boundaries. The simplest side boundaries are zero values, but these are generally rejected because people do not wish to assume data is zero beyond where it is measured. The most popular side conditions are not much more complicated, however. These are zero-slope side boundaries like those shown in Figure 6.
|
leakend
Figure 6 Pulses at various distances from a side boundary smoothed with two-sided leaky integration and zero-slope side conditions. Beyond the last value at the edge is a theoretical value that is the same as the edge value. |  |
I habitually smoothed with damped exponentials, but I switched to triangles after I encountered several examples where the exponential tails decreased too slowly.
The analysis for double-sided damped leaky integration with zero-slope boundaries
is found in my previous books and elsewhere,
so here I will simply state the result and leave you with
a working program.
This kind of integration
arises in the numerical solution of wave equations.
Mathematically, it means solving
![]() for V(x) given U(x).
In the limit of small
for V(x) given U(x).
In the limit of small ![]() , the operation is simply double integration.
Nonzero
, the operation is simply double integration.
Nonzero ![]() makes it leaky integration.
makes it leaky integration.
The operation looks like the Helmholtz equation of physics
but is not, because we take ![]() for damped solutions,
whereas the Helmholtz equation typically takes
for damped solutions,
whereas the Helmholtz equation typically takes ![]() for oscillating wave solutions.
Figure 6 was created with
leaky(), which performs the smoothing task
using a double-sided exponential response
with a decay to amplitude e-1 in a given distance.
It invokes the routine tris(),
a solver of tridiagonal simultaneous equations,
which is explained in FGDP.
for oscillating wave solutions.
Figure 6 was created with
leaky(), which performs the smoothing task
using a double-sided exponential response
with a decay to amplitude e-1 in a given distance.
It invokes the routine tris(),
a solver of tridiagonal simultaneous equations,
which is explained in FGDP.
# keyword: tridiagonal smoothing on 1-axis or 2-axis
subroutine leaky( distance, m1, n12, uu, vv )
integer i, m1, n12
real distance # input: 1. < distance < infinity
real uu(m1,n12) # data in is the vector (uu( 1, i), i=1,n12)
real vv(m1,n12) # data out is the vector (vv( 1, i), i=1,n12)
real a, b, dc, side
temporary real vecin( n12), vecout( n12)
a = - (1.-1./distance); b = 1.+a*a; dc = b+a+a
a = a/dc; b = b/dc; side = a + b
do i= 1,n12 { vecin(i) = uu(1,i)}
if( distance<=1.|| n12==1) {call copy( n12, vecin, vecout)}
else {call tris( n12, side, a, b, a, side, vecin, vecout)}
do i= 1,n12 { vv(1,i) = vecout(i) }
return; end
# tridiagonal simultaneous equations as in FGDP and IEI
#
subroutine tris( n, endl, a, b, c, endr, d, t )
integer i, n
real endl, a, b, c, endr, d(n), t(n)
temporary real e(n), f(n), deni(n)
if( n == 1) { t(1) = d(1) / b; return }
e(1) = - a / endl
do i= 2, n-1 {
deni(i) = 1. / ( b + c * e(i-1) )
e(i) = - a * deni(i)
}
f(1) = d(1) / endl
do i= 2, n-1
f(i) = (d(i) - c * f(i-1)) * deni(i)
t(n) = ( d(n) - c * f(n-1) ) / ( endr + c * e(n-1) )
do i= n-1, 1, -1
t(i) = e(i) * t(i+1) + f(i)
return; end
It is convenient to refer to the symmetrical double integration
operator as ![]() , where the superscripts denote integration,
in contrast to the usual subscripts, which denote
differentiation.
Since differentiation is widely regarded as an odd operator,
it is natural also to define the odd integration operator
, where the superscripts denote integration,
in contrast to the usual subscripts, which denote
differentiation.
Since differentiation is widely regarded as an odd operator,
it is natural also to define the odd integration operator
![]() .
.