




Next: Damped solution
Up: HOW TO DIVIDE NOISY
Previous: HOW TO DIVIDE NOISY
Think of any real numbers x, y, and f
and any program containing x=y/f.
How can we change the program so that it never divides by zero?
A popular answer is to change x=y/f
to 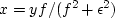 , where
, where  is any tiny value.
When
is any tiny value.
When 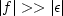 ,then x is approximately y/f as expected.
But when the divisor f vanishes,
the result is safely zero instead of infinity.
The transition is smooth,
but some criterion is needed to choose the value of
,then x is approximately y/f as expected.
But when the divisor f vanishes,
the result is safely zero instead of infinity.
The transition is smooth,
but some criterion is needed to choose the value of  .This method may not be the only way or the best way
to cope with
zero division,
but it is a good way,
and it permeates the subject of signal analysis.
.This method may not be the only way or the best way
to cope with
zero division,
but it is a good way,
and it permeates the subject of signal analysis.
To apply this method in the Fourier domain,
suppose X, Y, and F are complex numbers.
What do we do then with X=Y/F?
We multiply the
top and bottom by the complex conjugate 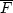 ,and again add
,and again add 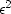 to the denominator.
Thus,
to the denominator.
Thus,
| 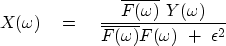 |
(12) |
Now the denominator must always be a positive number greater than zero,
so division is always safe.
In preparing figures with equation (12),
I learned that it is helpful to recast the equation in a scaled form.
First replace 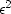 ,which has physical units of |F|2,
by
,which has physical units of |F|2,
by 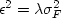 , where
, where
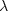 is a dimensionless parameter
and
is a dimensionless parameter
and 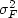 is the average value of
is the average value of 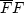 .Then I rescaled equation (12) to
.Then I rescaled equation (12) to
| 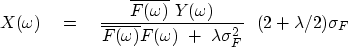 |
(13) |
The result is that the scale of X is independent
of the scale of F and the scale of 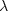 .This facilitates plotting X over a range of those parameters.
I found the 2s in the expression by experimentation.
Of course, if the plotting software you are using
adjusts a scale factor to fill a defined area,
then the scaling may be unimportant.
Equation (13) ranges continuously from
inverse filtering with
.This facilitates plotting X over a range of those parameters.
I found the 2s in the expression by experimentation.
Of course, if the plotting software you are using
adjusts a scale factor to fill a defined area,
then the scaling may be unimportant.
Equation (13) ranges continuously from
inverse filtering with
X=Y/F to filtering with
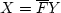 ,which is called ``matched filtering.''
,which is called ``matched filtering.''
Notice that for any complex number F,
the phase of 1/F equals the phase of 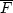 ,so all these filters have the same phase.
,so all these filters have the same phase.
The filter 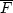 is called the ``matched filter."
If nature created Y by random bursts of energy into F,
then building X from Y and F
by choosing
is called the ``matched filter."
If nature created Y by random bursts of energy into F,
then building X from Y and F
by choosing 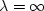 in equation (13)
amounts to
in equation (13)
amounts to 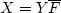 which crosscorrelates F with
the randomly placed copies of F that are in Y.
which crosscorrelates F with
the randomly placed copies of F that are in Y.





Next: Damped solution
Up: HOW TO DIVIDE NOISY
Previous: HOW TO DIVIDE NOISY
Stanford Exploration Project
10/21/1998
![]() ,and again add
,and again add ![]() to the denominator.
Thus,
to the denominator.
Thus,
![]() ,which has physical units of |F|2,
by
,which has physical units of |F|2,
by ![]() , where
, where
![]() is a dimensionless parameter
and
is a dimensionless parameter
and ![]() is the average value of
is the average value of ![]() .Then I rescaled equation (12) to
.Then I rescaled equation (12) to
![]() ,which is called ``matched filtering.''
,which is called ``matched filtering.''
![]() ,so all these filters have the same phase.
,so all these filters have the same phase.
![]() is called the ``matched filter."
If nature created Y by random bursts of energy into F,
then building X from Y and F
by choosing
is called the ``matched filter."
If nature created Y by random bursts of energy into F,
then building X from Y and F
by choosing ![]() in equation (13)
amounts to
in equation (13)
amounts to ![]() which crosscorrelates F with
the randomly placed copies of F that are in Y.
which crosscorrelates F with
the randomly placed copies of F that are in Y.