 |
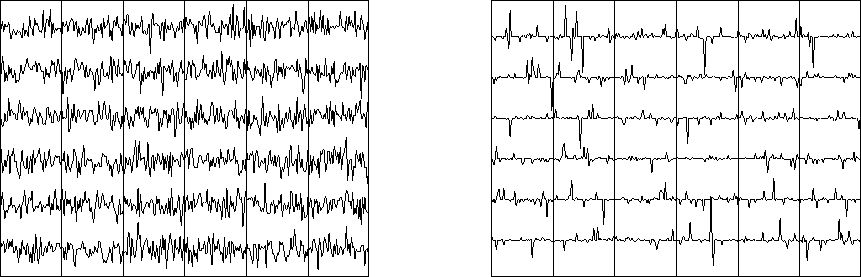
Figure 4 Left are random numbers from a Gaussian probability function. (The random numbers are connected by lines.) Right, the random numbers are cubed, making a signal in which large spikes are sparser.
can be modeled in many ways, two of which are (1) that many points can have zero value (or a value that is smaller than expected from a Gaussian); and (2) that the Gaussian probability function describes the many smaller values, but some larger values also occur from time to time.
It turns out that the Gaussian probability function generates more cryptic signals than any other probability function. It also turns out that theory is best developed for the Gaussian case. Thus, Gaussian theory, which is the most pessimistic, tends to be applied to both Gaussian and sparser data. Sparse signals derive from diverse models, and usually there is not enough information to establish a convincing model. In practical work, ``non-Gaussian'' generally means ``sparser than Gaussian.'' Figure 4 illustrates random signals from a Gaussian probability function and a sparser signal made by cubing the random numbers that emerge from a Gaussian random-number generator.
 |