For real ![]() , a plot of real and imaginary parts of Z is the circle
, a plot of real and imaginary parts of Z is the circle
![]() .A smaller circle is .9Z.
A right-shifted circle is 1+.9Z.
Let Z0 be a complex number, such as
x0+iy0, or
.A smaller circle is .9Z.
A right-shifted circle is 1+.9Z.
Let Z0 be a complex number, such as
x0+iy0, or
![]() ,where
,where ![]() and
and ![]() are fixed constants.
Consider the complex Z plane for the two-term filter
are fixed constants.
Consider the complex Z plane for the two-term filter
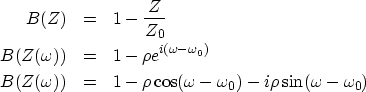 |
(34) | |
| (35) | ||
| (36) |
 |
Real and imaginary parts of B are plotted in Figure 18.
Arrows are at frequency ![]() intervals of
intervals of ![]() .Observe that for
.Observe that for ![]() the sequence of arrows
has a sequence of angles that ranges over
the sequence of arrows
has a sequence of angles that ranges over ![]() ,whereas for
,whereas for ![]() the sequence of arrows
has a sequence of angles between
the sequence of arrows
has a sequence of angles between ![]() .Now let us replot equation (37)
in a more conventional way, with
.Now let us replot equation (37)
in a more conventional way, with ![]() as the horizontal axis.
Whereas the phase is the angle of an arrow in Figure 18,
in Figure 19 it is the arctangent of
as the horizontal axis.
Whereas the phase is the angle of an arrow in Figure 18,
in Figure 19 it is the arctangent of ![]() .
Notice how different is the phase curve in
Figure 19 for
.
Notice how different is the phase curve in
Figure 19 for ![]() than for
than for ![]() .
.
Real and imaginary parts of B
are periodic functions of the frequency ![]() ,since
,since ![]() .We might be tempted to conclude that the phase
would be periodic too.
Figure 19 shows, however, that for a nonminimum-phase filter,
as
.We might be tempted to conclude that the phase
would be periodic too.
Figure 19 shows, however, that for a nonminimum-phase filter,
as ![]() ranges from
ranges from ![]() to
to ![]() ,the phase
,the phase ![]() increases by
increases by ![]() (because the circular path in Figure 18 surrounds the origin).
To make Figure 19 I used the Fortran arctangent function
that takes two arguments, x, and y.
It returns an angle between
(because the circular path in Figure 18 surrounds the origin).
To make Figure 19 I used the Fortran arctangent function
that takes two arguments, x, and y.
It returns an angle between ![]() and
and ![]() .As I was plotting the nonminimum phase,
the phase suddenly jumped discontinuously
from a value near
.As I was plotting the nonminimum phase,
the phase suddenly jumped discontinuously
from a value near ![]() to
to ![]() , and I needed to add
, and I needed to add ![]() to keep the curve continuous.
This is called ``phase unwinding.''
to keep the curve continuous.
This is called ``phase unwinding.''
|
phase
Figure 19 Left shows real and imaginary parts and phase angle of equation ((37)), for | 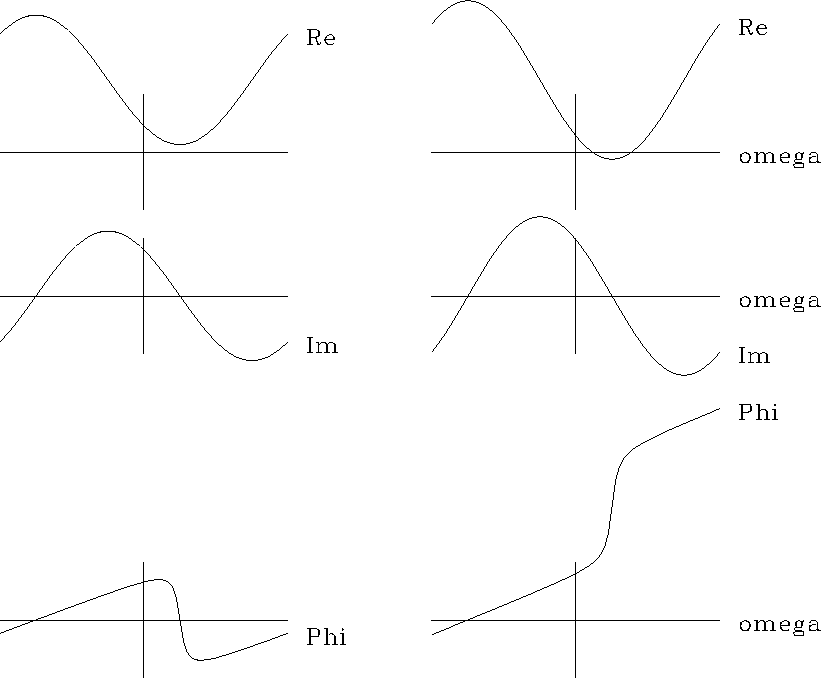 |
You would use phase unwinding
if you ever had to solve the following problem:
given an earthquake at location (x,y), did it occur
in country X?
You would circumnavigate the country--compare
the circle in Figure 18--and see if the phase angle
from the earthquake to the country's boundary accumulated to (yes)
or to ![]() (no).
(no).
The word ``minimum" is used in ``minimum phase"
because delaying a filter can always add more phase.
For example,
multiplying any polynomial by Z delays it and adds ![]() to its phase.
to its phase.
For the minimum-phase filter,
the group delay ![]() applied to Figure 19
is a periodic function of
applied to Figure 19
is a periodic function of ![]() .For the nonminimum-phase filter, group delay
happens to be a monotonically increasing function of
.For the nonminimum-phase filter, group delay
happens to be a monotonically increasing function of ![]() .Since it is not an all-pass filter, the monotonicity is accidental.
.Since it is not an all-pass filter, the monotonicity is accidental.
Because group delay ![]() is the Fourier dual
to instantaneous frequency
is the Fourier dual
to instantaneous frequency ![]() ,we can now go back to Figure 5 and explain
the discontinuous behavior of instantaneous frequency
where the signal amplitude is near zero.
,we can now go back to Figure 5 and explain
the discontinuous behavior of instantaneous frequency
where the signal amplitude is near zero.