




Next: References
Up: TOMOGRAPHY AND OTHER APPLICATIONS
Previous: Clash in philosophies
A theory exists for general constraints in quadratic form minimization.
I have not found the theory to be useful
in any application I have run into so far,
but it should come in handy for writing erudite theoretical articles.
Constraint equations are an underdetermined set of equations,
say 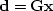 (the number of components in
(the number of components in  exceeds that in
exceeds that in 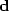 ),
which must be solved exactly
while some other set is solved in the
least-squares
sense,
say
),
which must be solved exactly
while some other set is solved in the
least-squares
sense,
say 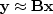 .This is formalized as
.This is formalized as
| ![\begin{displaymath}
\min_{\bold x} \ \{ Q_C(\bold x) \ =\ \lim_{\epsilon \righta...
...on}
(\bold d - \bold G\bold x)'
(\bold d - \bold G\bold x)
] \}\end{displaymath}](img76.gif) |
(15) |
In my first book (FGDP: see page 113),
I minimized QC by power series, letting
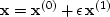 , and hence
, and hence
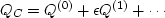 .I minimized both Q(0) and Q(1)
with respect to
.I minimized both Q(0) and Q(1)
with respect to
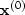 and
and 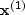 .After a page of algebra, this approach leads to the system of equations
.After a page of algebra, this approach leads to the system of equations
| ![\begin{displaymath}
\left[
\begin{array}
{cc}
\bold B'\bold B & \bold G' \ ...
...{array}
{c}
\bold B' \bold y \
\bold d \end{array} \right]\end{displaymath}](img81.gif) |
(16) |
where 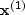 has been superseded by the variable
has been superseded by the variable
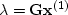 ,which has fewer components than
,which has fewer components than 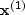 ,and where
,and where 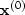 has simply been replaced by
has simply been replaced by  .The second of the two equations shows that
the constraints are satisfied.
But it is not obvious
from equation (16)
that (15) is minimized.
.The second of the two equations shows that
the constraints are satisfied.
But it is not obvious
from equation (16)
that (15) is minimized.
The great mathematician Lagrange apparently looked at the result,
equation (16), and realized that he could arrive at it
far more simply by extremalizing the following quadratic form:
| 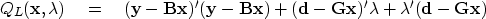 |
(17) |
We can quickly verify that Lagrange was correct
by setting to zero the derivatives with respect to
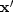 and
and 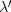 .Naturally, everyone prefers to handle constraints by Lagrange's method.
Unfortunately, Lagrange failed
to pass on to the teachers of this world an intuitive reason
why
extremalizing (17)
gives the same result as
extremalizing (15).
Lagrange's quadratic form is not even positive definite
(that is, it cannot be written as something times its adjoint).
In honor of Lagrange,
the variables
.Naturally, everyone prefers to handle constraints by Lagrange's method.
Unfortunately, Lagrange failed
to pass on to the teachers of this world an intuitive reason
why
extremalizing (17)
gives the same result as
extremalizing (15).
Lagrange's quadratic form is not even positive definite
(that is, it cannot be written as something times its adjoint).
In honor of Lagrange,
the variables 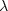 have come to be known as Lagrange multipliers.
have come to be known as Lagrange multipliers.





Next: References
Up: TOMOGRAPHY AND OTHER APPLICATIONS
Previous: Clash in philosophies
Stanford Exploration Project
10/21/1998
![]() (the number of components in
(the number of components in ![]() exceeds that in
exceeds that in ![]() ),
which must be solved exactly
while some other set is solved in the
least-squares
sense,
say
),
which must be solved exactly
while some other set is solved in the
least-squares
sense,
say ![]() .This is formalized as
.This is formalized as