




Next: Relation of missing data
Up: Missing-data restoration
Previous: Missing-data restoration
In its simplest form,
the Nyquist condition says that
we can have no frequencies higher than two points per wavelength.
In migration, this is a strong constraint on data collection.
It seems there is no escape.
Yet, in applications dealing with a CMP gather
(such as in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) or
or ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ),
we see data with spatial frequencies that exceed Nyquist
and we are not bothered, because after NMO,
these frequencies are OK.
Nevertheless, such data is troubling because
it breaks many of our conventional programs,
such as downward continuation with finite differences
or with Fourier transforms.
(No one uses focusing for stacking.)
Since NMO defies the limitation imposed
by the simple statement of the Nyquist condition,
we revise the condition to say that
the real limitation is on the spectral bandwidth,
not on the maximum frequency.
Mr. Nyquist does not tell us where that bandwidth must be located.
Further, it seems that precious bandwidth need not be contiguous.
The signal's spectral band can be split into pieces
and those pieces positioned in different places.
Fundamentally, the issue is whether the total bandwidth exceeds Nyquist.
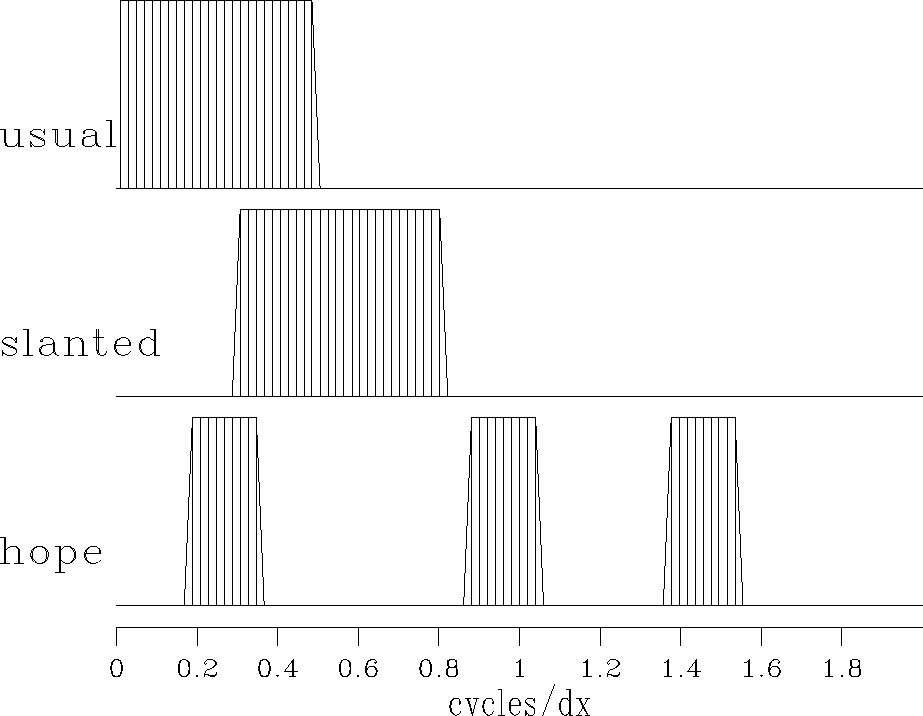
Noncontiguous Nyquist bands are depicted in Figure 1.
),
we see data with spatial frequencies that exceed Nyquist
and we are not bothered, because after NMO,
these frequencies are OK.
Nevertheless, such data is troubling because
it breaks many of our conventional programs,
such as downward continuation with finite differences
or with Fourier transforms.
(No one uses focusing for stacking.)
Since NMO defies the limitation imposed
by the simple statement of the Nyquist condition,
we revise the condition to say that
the real limitation is on the spectral bandwidth,
not on the maximum frequency.
Mr. Nyquist does not tell us where that bandwidth must be located.
Further, it seems that precious bandwidth need not be contiguous.
The signal's spectral band can be split into pieces
and those pieces positioned in different places.
Fundamentally, the issue is whether the total bandwidth exceeds Nyquist.
Noncontiguous Nyquist bands are depicted in Figure 1.
nytutor
Figure 1
Hypothetical spatial frequency bands.
Top is typical.
Middle for data skewed with 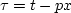 . Bottom depicts data with wave arrivals
from three directions. . Bottom depicts data with wave arrivals
from three directions.
|
|  |





Noncontiguous bandwidth arises naturally with
two-dimensional data where there are several plane waves present.
There the familiar spatial Nyquist limitation
oversimplifies real life because the plane waves link time and space.
|
The spatial Nyquist frequency need not limit
the analysis of seismic data
because the plane-wave model links space with time.
|





Next: Relation of missing data
Up: Missing-data restoration
Previous: Missing-data restoration
Stanford Exploration Project
10/21/1998
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) or
or ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ),
we see data with spatial frequencies that exceed Nyquist
and we are not bothered, because after NMO,
these frequencies are OK.
Nevertheless, such data is troubling because
it breaks many of our conventional programs,
such as downward continuation with finite differences
or with Fourier transforms.
(No one uses focusing for stacking.)
Since NMO defies the limitation imposed
by the simple statement of the Nyquist condition,
we revise the condition to say that
the real limitation is on the spectral bandwidth,
not on the maximum frequency.
Mr. Nyquist does not tell us where that bandwidth must be located.
Further, it seems that precious bandwidth need not be contiguous.
The signal's spectral band can be split into pieces
and those pieces positioned in different places.
Fundamentally, the issue is whether the total bandwidth exceeds Nyquist.
Noncontiguous Nyquist bands are depicted in Figure 1.
),
we see data with spatial frequencies that exceed Nyquist
and we are not bothered, because after NMO,
these frequencies are OK.
Nevertheless, such data is troubling because
it breaks many of our conventional programs,
such as downward continuation with finite differences
or with Fourier transforms.
(No one uses focusing for stacking.)
Since NMO defies the limitation imposed
by the simple statement of the Nyquist condition,
we revise the condition to say that
the real limitation is on the spectral bandwidth,
not on the maximum frequency.
Mr. Nyquist does not tell us where that bandwidth must be located.
Further, it seems that precious bandwidth need not be contiguous.
The signal's spectral band can be split into pieces
and those pieces positioned in different places.
Fundamentally, the issue is whether the total bandwidth exceeds Nyquist.
Noncontiguous Nyquist bands are depicted in Figure 1.