 |
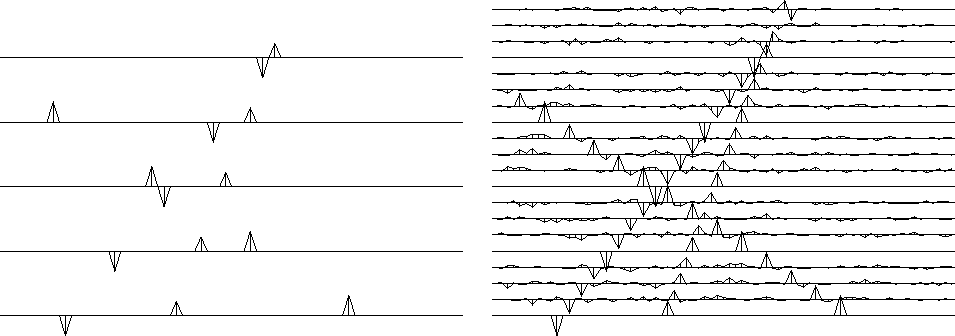
Figure 13 Left is five signals, each showing three arrivals. Using the data shown on the left (and no more), the signals have been interpolated. Three new traces appear between each given trace as shown on the right.
 |
Figure 13 shows three plane waves recorded on five channels and the interpolated data. Both the original data and the interpolated data can be described as ``beyond aliasing'' because on the input data the signal shifts exceed the signal duration. The calculation requires only a few seconds of a ``two-stage least-squares'' method, where the first stage estimates an inverse covariance matrix of the known data, and the second uses it to estimate the missing traces. Actually, a 2-D prediction-error filter
is estimated, and the inverse covariance matrix, which amounts to the PE filter times its adjoint, is not needed explicitly.
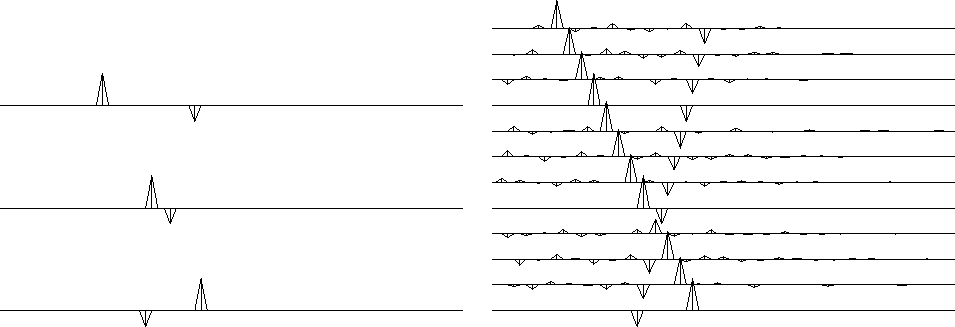 |
Let us now examine a case with minimal complexity. Figure 14 shows two plane waves recorded on three channels. That is the minimum number of channels required to distinguish two superposing plane waves. Notice on the interpolated data that the original traces are noise-free, but the new traces have acquired a low level of noise. This will be dealt with later.
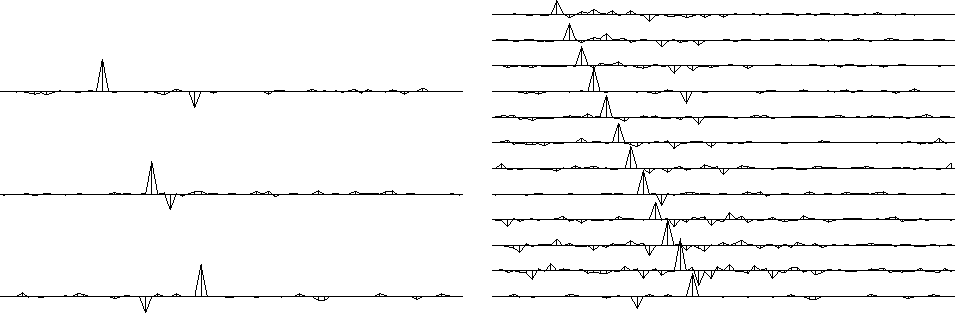
Figure 15 shows the same calculation in the presence of noise on the original data. We see that the noisy data is interpolatable just as was the noise-free data, but now we can notice the organization of the noise. It has the same slopes as the plane waves. This was also true on the earlier figures (Figure 13 and 14), as is more apparent if you look at the page from various grazing angles. To display the slopes more clearly, Figure 15 is redisplayed in a raster mode in Figure 16.
 |
 |