subroutine slowft( adj, add, nyq, t0,dt,nt,tt, f0,df, nf,ff)
integer it,ie, adj, add, nyq, nt, nf
complex cexp, cmplx, tt(nt), ff(nf)
real pi2, freq, time, scale, t0,dt, f0,df
call adjnull( adj, add, tt,2*nt, ff,2*nf)
pi2= 2. * 3.14159265; scale = 1./sqrt( 1.*nt)
df = (1./dt) / nf
if( nyq>0)
f0 = - .5/dt
else
f0 = - .5/dt + df/2.
do ie = 1, nf { freq= f0 + df*(ie-1)
do it = 1, nt { time= t0 + dt*(it-1)
if( adj == 0 )
ff(ie)= ff(ie) + tt(it) * cexp(cmplx(0., pi2*freq*time)) * scale
else
tt(it)= tt(it) + ff(ie) * cexp(cmplx(0.,-pi2*freq*time)) * scale
}}
return; end
The total frequency band is
![]() radians per sample unit
or
radians per sample unit
or ![]() Hz.
Dividing the total interval by the number of points nf gives
Hz.
Dividing the total interval by the number of points nf gives ![]() .We could choose the frequencies to run from 0 to
.We could choose the frequencies to run from 0 to ![]() radians/sample.
That would work well for many applications,
but it would be a nuisance for applications such as differentiation
in the frequency domain, which require multiplication by
radians/sample.
That would work well for many applications,
but it would be a nuisance for applications such as differentiation
in the frequency domain, which require multiplication by ![]() including the negative frequencies
as well as the positive.
So it seems more natural to begin at the most negative frequency
and step forward to the most positive frequency.
Next, we must make a confusing choice.
including the negative frequencies
as well as the positive.
So it seems more natural to begin at the most negative frequency
and step forward to the most positive frequency.
Next, we must make a confusing choice.
Refer to Figure 1.
We could begin the frequency axis at the negative Nyquist,
![]() Hz;
then we would finish one point short of the positive Nyquist.
This is shown on the left two circles in Figure 1.
Alternately, for the right two circles
we could shift by half a mesh interval,
so the points would straddle the
Nyquist frequency.
To do this, the most negative frequency would have to be
Hz;
then we would finish one point short of the positive Nyquist.
This is shown on the left two circles in Figure 1.
Alternately, for the right two circles
we could shift by half a mesh interval,
so the points would straddle the
Nyquist frequency.
To do this, the most negative frequency would have to be
![]() Hz.
In routine slowft() and in the test results,
``nyq=1'' is a logical statement
that the Nyquist frequency is in the dataset.
Oppositely, if the Nyquist frequency is interlaced
by the given frequencies, then nyq=0.
Finally, the heart of the program is to compute either a Fourier sum,
or its inverse, which uses the complex conjugate.
Hz.
In routine slowft() and in the test results,
``nyq=1'' is a logical statement
that the Nyquist frequency is in the dataset.
Oppositely, if the Nyquist frequency is interlaced
by the given frequencies, then nyq=0.
Finally, the heart of the program is to compute either a Fourier sum,
or its inverse, which uses the complex conjugate.
The routine ftlagslow() below
simply transforms a signal to the Fourier domain,
multiplies by ![]() , where
t0 is some desired time lag,
and then inverse transforms to the time domain.
Notice that if the negative Nyquist frequency is present,
it is treated as the average of the negative and positive
Nyquist frequencies.
If we do not take special care to do this,
we will be disappointed to find that the time derivative
of a real-time function develops an imaginary part.
, where
t0 is some desired time lag,
and then inverse transforms to the time domain.
Notice that if the negative Nyquist frequency is present,
it is treated as the average of the negative and positive
Nyquist frequencies.
If we do not take special care to do this,
we will be disappointed to find that the time derivative
of a real-time function develops an imaginary part.
call slowft( 0, 0, nyq, t0, dt, n1, ctt, f0, df, n1, cff)
do ie= 1, n1 { freq= f0 + (ie-1)*df
if( ie==1 && nyq > 0)
cff(1) = cff(1) * cos( 2.*3.14159265 * freq * lag )
else
cff(ie) = cff(ie) * cexp( cmplx(0., 2.*3.14159265 * freq * lag))
}
call slowft( 1, 0, nyq, t0, dt, n1, ctt, f0, df, n1, cff)
return; end
subroutine ftlagslow( nyq, lag, t0,dt, n1, ctt)
integer nyq, n1, ie
real lag, t0, dt, f0, df, freq
complex ctt(n1), cexp, cmplx
temporary complex cff(n1)
Figure 4 shows what happens when an impulse is shifted by various fractions of a sample unit with subroutine ftlagslow(). Notice that during the delay, the edges of the signals ripple--this is sometimes called the ``Gibbs ripple.'' You might find these ripples annoying, but it is not easy to try to represent an impulse halfway between two mesh points. You might think of doing so with (.5,.5), but that lacks the high frequencies of an ideal impulse.
|
delay
Figure 3 An impulse function delayed various fractions of a mesh point. Pushbutton for interaction (experimental). | 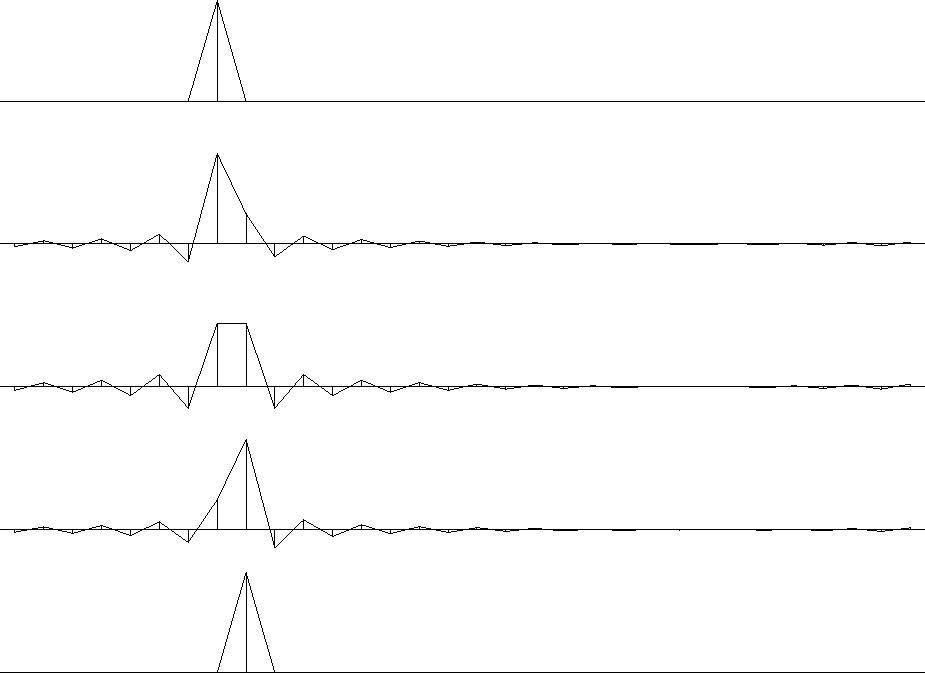 |
The routine ftderivslow() below
is the Fourier-domain routine
for computing a time derivative
by multiplying in the frequency domain by
do ie= 1, ntf { freq= f0+(ie-1)*df
cff(ie) = cff(ie) * cmplx( 0., - 2. * 3.141549265 * freq )
}
if( nyq > 0 ) # if( omega0 == -pi/dt)
cff(1) = 0.
call slowft( 1, 0, nyq, t0, dt, ntf, cdd, f0, df, ntf, cff)
return; end
![]() .
.
subroutine ftderivslow( nyq, t0,dt, ntf, ctt, cdd)
integer nyq, ntf, ie
real t0,dt,f0,df, freq
complex ctt(ntf), cdd(ntf), cmplx
temporary complex cff(ntf)
call slowft( 0, 0, nyq, t0, dt, ntf, ctt, f0, df, ntf, cff)