|
box2triangle
Figure 7 Top shows a rectangle transformed to a sinc. Bottom shows the sinc squared, back transformed to a triangle. | 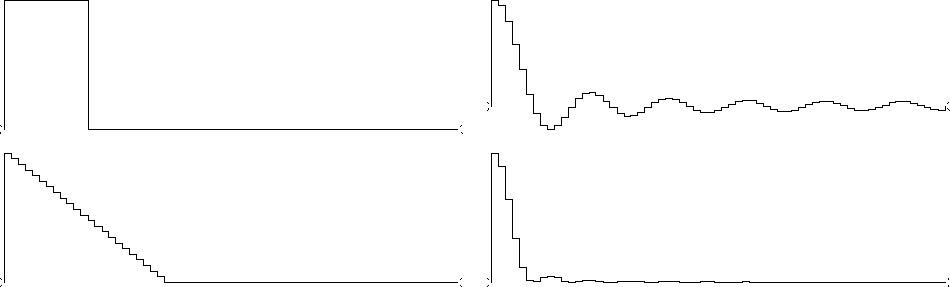 |
An example is shown in Figure 8. It is the result of a Fourier-domain computation which shows that the convolution of a rectangle function with itself gives a triangle. Notice that the triangle is clean--there are no unexpected end effects.
|
box2triangle
Figure 7 Top shows a rectangle transformed to a sinc. Bottom shows the sinc squared, back transformed to a triangle. |  |
Because of the fast method of Fourier transform described next, the frequency-domain calculation is quicker when both X(Z) and B(Z) have more than roughly 20 coefficients. If either X(Z) or B(Z) has less than roughly 20 coefficients, then the time-domain calculation is quicker.