|
triv1
Figure 1 A continuous signal sampled at uniform time intervals. (Press button for trivial interaction with plot.) | 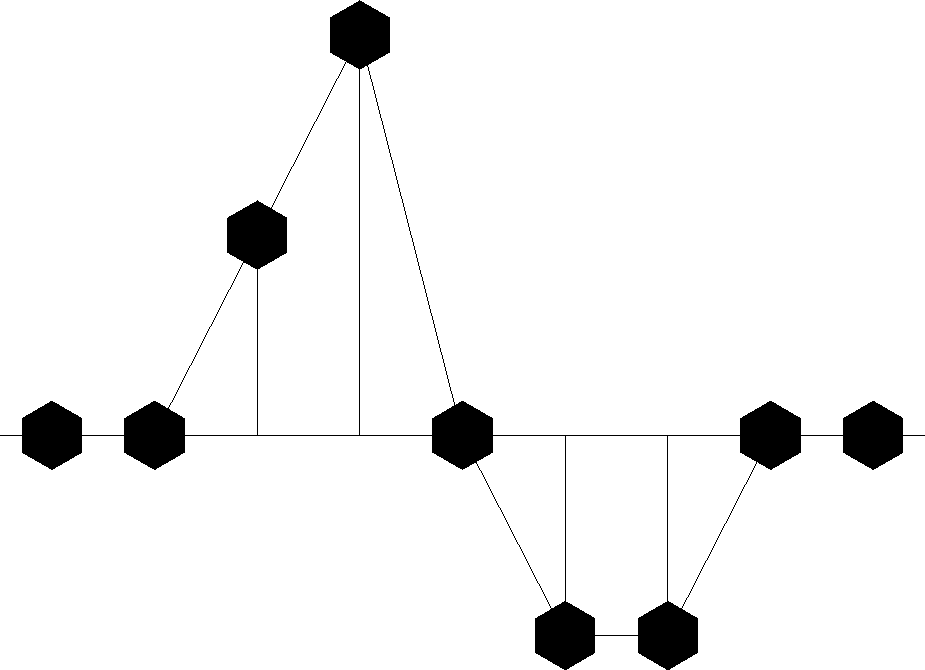 |
|
triv1
Figure 1 A continuous signal sampled at uniform time intervals. (Press button for trivial interaction with plot.) |  |
To analyze such an observed signal in a computer, it is necessary to approximate it in some way by a list of numbers. The usual way to do this is to evaluate or observe b(t) at a uniform spacing of points in time, call this discretized signal bt. For Figure 1, such a discrete approximation to the continuous function could be denoted by the vector
| (1) |
Another way to represent a signal is as a polynomial, where the coefficients of the polynomial represent the value of bt at successive times. For example,
| |
(2) |
|
triv2
Figure 2 The coefficients of ZB(Z) are the shifted version of the coefficients of B(Z). | 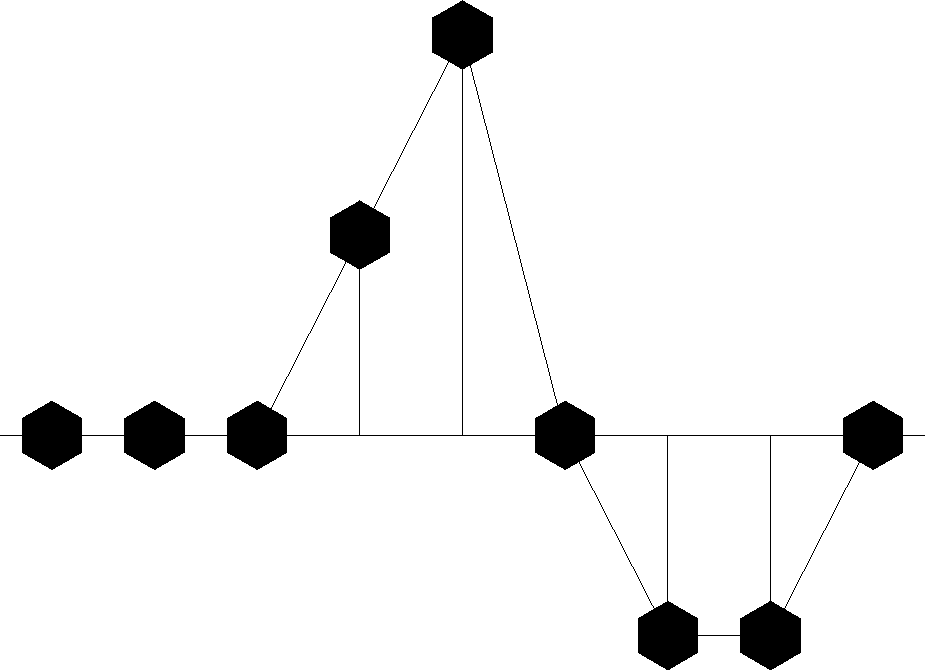 |
Figure 2 shows the same waveform as Figure 1, but now the waveform has been delayed. So the signal bt is delayed n time units by multiplying B(Z) by Zn. The delay operator Z is important in analyzing waves simply because waves take a certain amount of time to move from place to place.
Another value of the delay operator is that it may be used to build up more complicated signals from simpler ones. Suppose bt represents the acoustic pressure function or the seismogram observed after a distant explosion. Then bt is called the ``impulse response.'' If another explosion occurred at t = 10 time units after the first, we would expect the pressure function y(t) depicted in Figure 3. In terms of Z-transforms, this pressure function would be expressed as Y(Z) = B(Z) + Z10 B(Z).
|
triv3
Figure 3 Response to two explosions. |  |