 |
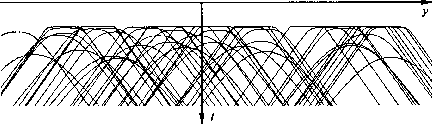
Figure 19 Constant-offset section over random point scatterers.
Figure 19 shows a synthetic constant-offset section (COS) taken from an earth model containing about fifty randomly placed point scatterers.
 |
Late arrival times appear hyperbolic. Earlier arrivals have flattened tops. The earliest possible arrival corresponds to a ray going horizontally from the shot to the geophone.
Figure 20 shows a synthetic common-shot profile (CSP) from the same earth model of random point scatterers.
|
randcsp
Figure 20 Common-shot profile over random point scatterers. | 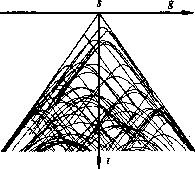 |
Each scatterer produces a hyperbolic arrival.
The hyperbolas are not symmetric around zero offset;
their locations are random. They must, however, all
lie under the lines ![]() .Hyperbolas with sharp tops can be found at late times as well as early times.
However, the sharp tops,
which are from shallow scatterers near the geophone,
must lie near the lines
.Hyperbolas with sharp tops can be found at late times as well as early times.
However, the sharp tops,
which are from shallow scatterers near the geophone,
must lie near the lines ![]() .
.
The left side of Figure 21 shows a synthetic common-midpoint gather (CMP) from an earth model containing about fifty randomly placed point scatterers.
 |
Because this is a common-midpoint gather, the curves are symmetric through zero offset. (The negative offsets of field data are hardly ever plotted). Some of the arrivals have flattened tops, which indicate scatterers that are not directly under the midpoint.
Normal-moveout (NMO) correction is a stretching of the data to try to flatten the hyperbolas. This correction assumes flat beds, but it also works for point scatterers that are directly under the midpoint. The right side of Figure 21 shows what happens when normal-moveout correction is applied on the random scatterer model. Some reflectors are flattened; others are ``overcorrected.''