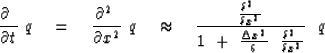Next: Time and depth derivatives
Up: FREQUENCY DISPERSION IN WAVE-MIGRATION
Previous: Second space derivatives
Increased absolute accuracy may always be purchased by reducing 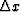 .Increased accuracy relative to the Nyquist frequency
may be purchased at a cost of computer time and analytical clumsiness by
adding higher-order terms, say,
.Increased accuracy relative to the Nyquist frequency
may be purchased at a cost of computer time and analytical clumsiness by
adding higher-order terms, say,
| 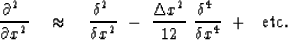 |
(37) |
As 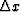 tends to zero (37) tends to the basic definitions
(30) and (31).
Coefficients like the 1/12 in (37)
may be determined by the Taylor-series
method if great accuracy is desired at small k.
Or somewhat different coefficients may be determined by curve-fitting
techniques if accuracy is desired over some range of k.
In practice (37) is hardly ever used, because there is a less
obvious expression that offers much more accuracy at less cost!
The idea is indicated by
tends to zero (37) tends to the basic definitions
(30) and (31).
Coefficients like the 1/12 in (37)
may be determined by the Taylor-series
method if great accuracy is desired at small k.
Or somewhat different coefficients may be determined by curve-fitting
techniques if accuracy is desired over some range of k.
In practice (37) is hardly ever used, because there is a less
obvious expression that offers much more accuracy at less cost!
The idea is indicated by
| 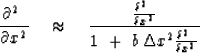 |
(38) |
where b is an adjustable constant.
The accuracy of (38) may be numerically evaluated
by substituting from (35) to get
| 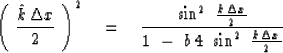 |
(39) |
The square root of (39)
is plotted in Figure 21 for a value of b = 1/6.
sixth
Figure 21
Accuracy of the second-derivative representation
equation (38)
and (39)
(for b=1/6) as a function of spatial wavenumber.
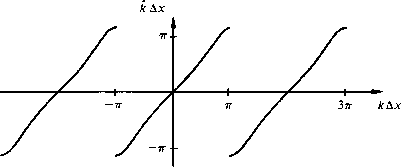
The sign of the square root of (39)
was chosen to agree with k
in the range 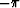 to
to  and to be
periodic outside the range. (Hale)
and to be
periodic outside the range. (Hale)

Taking b in (38) and (39) to be 1/12, then
(38), (39) and (37) would agree
to second order in 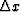 .The 1/12 comes from series expansion, but the 1/6 fits over a
wider range and is a value in common use.
Francis Muir has pointed out
that the value
.The 1/12 comes from series expansion, but the 1/6 fits over a
wider range and is a value in common use.
Francis Muir has pointed out
that the value 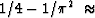 1/6.726 gives an
exact
fit at the Nyquist frequency and an accurate fit over all lower frequencies!
Few explorationists consider the remaining
accuracy deficiency of (38) and (39)
to be sufficient to warrant interpolation
of field-recorded values.
Figure 22 compares hyperbolas for various values of b.
Observe in Figure 22 that the longest wavelengths
travel at the same speed regardless of b.
The time axis in Figure 22 is only 256 points long,
whereas in practice it would be a thousand or more.
So Figure 22 exaggerates the frequency dispersion
attributable in practice to finite differencing the x-axis.
1/6.726 gives an
exact
fit at the Nyquist frequency and an accurate fit over all lower frequencies!
Few explorationists consider the remaining
accuracy deficiency of (38) and (39)
to be sufficient to warrant interpolation
of field-recorded values.
Figure 22 compares hyperbolas for various values of b.
Observe in Figure 22 that the longest wavelengths
travel at the same speed regardless of b.
The time axis in Figure 22 is only 256 points long,
whereas in practice it would be a thousand or more.
So Figure 22 exaggerates the frequency dispersion
attributable in practice to finite differencing the x-axis.
sixth5
Figure 22
Hyperbolas for 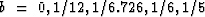 .
.





Let us be sure it is clear how (38) and (39) are put
into use.
Take b = 1/6.
The simplest prototype equation is the heat-flow equation:
| 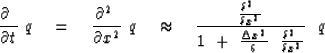 |
(40) |
Multiply through the denominator:
| 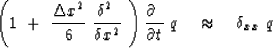 |
(41) |





Next: Time and depth derivatives
Up: FREQUENCY DISPERSION IN WAVE-MIGRATION
Previous: Second space derivatives
Stanford Exploration Project
10/31/1997
![]() .Increased accuracy relative to the Nyquist frequency
may be purchased at a cost of computer time and analytical clumsiness by
adding higher-order terms, say,
.Increased accuracy relative to the Nyquist frequency
may be purchased at a cost of computer time and analytical clumsiness by
adding higher-order terms, say,
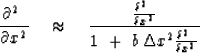
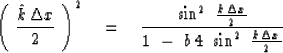
![]() .The 1/12 comes from series expansion, but the 1/6 fits over a
wider range and is a value in common use.
Francis Muir has pointed out
that the value
.The 1/12 comes from series expansion, but the 1/6 fits over a
wider range and is a value in common use.
Francis Muir has pointed out
that the value ![]() 1/6.726 gives an
exact
fit at the Nyquist frequency and an accurate fit over all lower frequencies!
Few explorationists consider the remaining
accuracy deficiency of (38) and (39)
to be sufficient to warrant interpolation
of field-recorded values.
Figure 22 compares hyperbolas for various values of b.
Observe in Figure 22 that the longest wavelengths
travel at the same speed regardless of b.
The time axis in Figure 22 is only 256 points long,
whereas in practice it would be a thousand or more.
So Figure 22 exaggerates the frequency dispersion
attributable in practice to finite differencing the x-axis.
1/6.726 gives an
exact
fit at the Nyquist frequency and an accurate fit over all lower frequencies!
Few explorationists consider the remaining
accuracy deficiency of (38) and (39)
to be sufficient to warrant interpolation
of field-recorded values.
Figure 22 compares hyperbolas for various values of b.
Observe in Figure 22 that the longest wavelengths
travel at the same speed regardless of b.
The time axis in Figure 22 is only 256 points long,
whereas in practice it would be a thousand or more.
So Figure 22 exaggerates the frequency dispersion
attributable in practice to finite differencing the x-axis.