




Next: Muir's rules for combining
Up: IMPEDANCE
Previous: Review of impedance filters
Begin with a function in discretized time pt.
The Fourier transform with the substitution 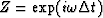 is the Z-transform
is the Z-transform
| 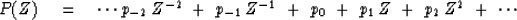 |
(29) |
Define 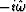 (which will turn out to be an approximation
to
(which will turn out to be an approximation
to 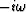 ) by
) by
| 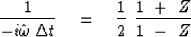 |
(30) |
Define another time function qt
with Z-transform Q(Z) by
applying the operator to P(Z):
| 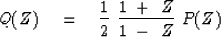 |
(31) |
Multiply both sides by (1-Z):
| 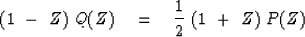 |
(32) |
Equate the coefficient of Zt on each side:
| 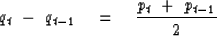 |
(33) |
Taking pt to be an impulse function,
we see that qt turns out
to be a step function, that is,
| 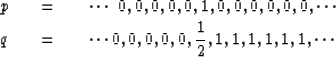 |
(34) |
| (35) |
So qt is the discrete domain representation of the integral
of pt from minus infinity to time t.
It is the same as a Crank-Nicolson-style numerical integration
of the differential equation dQ/dt = P.
The operator (1+Z)/(1-Z) is called the bilinear transform.
The accuracy of the approximation to differentiation
can be seen by multiplication on
top and bottom by Z-.5 and
substitution of 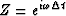 .
.
| 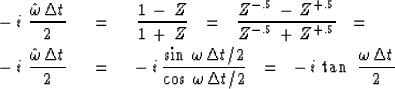 |
(36) |
| (37) |
The integration operator has a pole at Z = 1, which
is exactly on the unit circle.
This raises the possibility of the paradox of infinity.
In other words, there are other noncausal expansions too.
For example,
taking 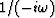 to be an imaginary, antisymmetric function
of
to be an imaginary, antisymmetric function
of 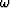 implies a real, antisymmetric time function,
namely,
implies a real, antisymmetric time function,
namely, 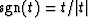 , which is not usually regarded
as the integration operator.
To avoid any ambiguity, we introduce here
a small positive number
, which is not usually regarded
as the integration operator.
To avoid any ambiguity, we introduce here
a small positive number  and define
and define 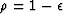 .The integration operator becomes
.The integration operator becomes
| 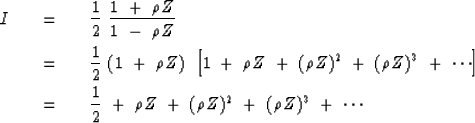 |
(38) |
| (39) |
| (40) |
Because 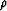 is slightly less than one, this series converges for any
value of Z on the unit circle.
If
is slightly less than one, this series converges for any
value of Z on the unit circle.
If  had been slightly negative instead of positive
the expansion would have come out in negative
instead of positive powers of Z.
had been slightly negative instead of positive
the expansion would have come out in negative
instead of positive powers of Z.
Now the big news is that the causal integration operator is an example
of an impedance function.
The operator is clearly causal with a causal inverse.
Let us check in the frequency domain that the real part is positive.
Rationalizing the denominator gives
| 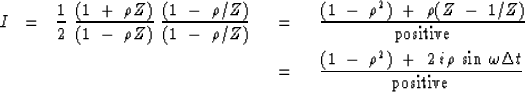 |
(41) |
| (42) |
Again, it is the choice of a positive  that has
caused
that has
caused 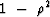 , and hence the real part
to be positive for all
, and hence the real part
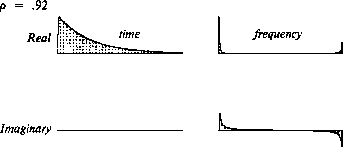
to be positive for all 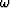 , as shown in Figure 5.
cintegral
, as shown in Figure 5.
cintegral
Figure 5
The causal integration operator I.
The frequency axis is represented by a discrete Fourier transform
over 256 points.
Zero time and zero frequency
are on the left end of their respective axes.

As multiplication by 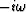 in
the frequency domain is associated
with differentiation d/dt in the time domain,
so is division by
in
the frequency domain is associated
with differentiation d/dt in the time domain,
so is division by 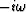 associated with integration.
People usually associate the
asymmetric operator (1,-1) with differentiation.
But notice that the inverse
to the causal integration operator, namely,
associated with integration.
People usually associate the
asymmetric operator (1,-1) with differentiation.
But notice that the inverse
to the causal integration operator, namely,
| 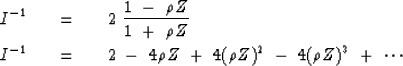 |
(43) |
| (44) |
also represents differentiation, although it is completely causal
and not at all asymmetric.
In linear systems analysis
this representation of discrete differentiation
is often the preferred one.
The construction of higher-order, stable differential
equations is subject to certain rules,
to be covered,
for combining impedances.
Occasionally it is necessary to have a
negative
real part for the differentiation operator.
This can be achieved by taking  to be negative, which means
taking
to be negative, which means
taking 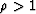 , and doing the infinite series expansion in
powers of Z-1, that is, anticausally instead of causally.
In either the anticausal or the causal
case the imaginary part will still be
, and doing the infinite series expansion in
powers of Z-1, that is, anticausally instead of causally.
In either the anticausal or the causal
case the imaginary part will still be 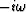 , but the real
part will have the opposite sign.
, but the real
part will have the opposite sign.





Next: Muir's rules for combining
Up: IMPEDANCE
Previous: Review of impedance filters
Stanford Exploration Project
10/31/1997
![]() is the Z-transform
is the Z-transform
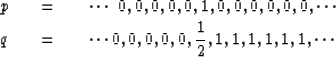
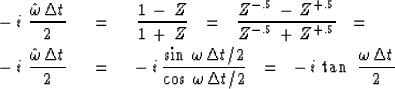
![]() to be an imaginary, antisymmetric function
of
to be an imaginary, antisymmetric function
of ![]() implies a real, antisymmetric time function,
namely,
implies a real, antisymmetric time function,
namely, ![]() , which is not usually regarded
as the integration operator.
To avoid any ambiguity, we introduce here
a small positive number
, which is not usually regarded
as the integration operator.
To avoid any ambiguity, we introduce here
a small positive number ![]() and define
and define ![]() .The integration operator becomes
.The integration operator becomes
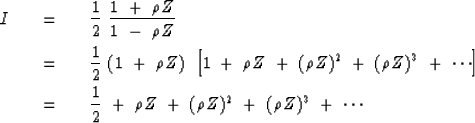
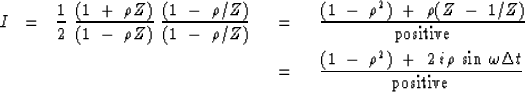
![]() in
the frequency domain is associated
with differentiation d/dt in the time domain,
so is division by
in
the frequency domain is associated
with differentiation d/dt in the time domain,
so is division by ![]() associated with integration.
People usually associate the
asymmetric operator (1,-1) with differentiation.
But notice that the inverse
to the causal integration operator, namely,
associated with integration.
People usually associate the
asymmetric operator (1,-1) with differentiation.
But notice that the inverse
to the causal integration operator, namely,
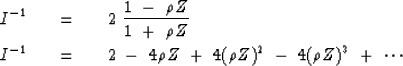
![]() to be negative, which means
taking
to be negative, which means
taking ![]() , and doing the infinite series expansion in
powers of Z-1, that is, anticausally instead of causally.
In either the anticausal or the causal
case the imaginary part will still be
, and doing the infinite series expansion in
powers of Z-1, that is, anticausally instead of causally.
In either the anticausal or the causal
case the imaginary part will still be ![]() , but the real
part will have the opposite sign.
, but the real
part will have the opposite sign.