|
hyptrunc
Figure 4 Hyperbolas truncated at a particular time. | 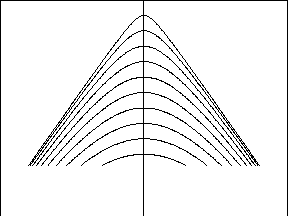 |
Figure 4 shows a family of hyperbolas.
|
hyptrunc
Figure 4 Hyperbolas truncated at a particular time. |  |
Notice that these hyperbolas do not extend to infinite time but they truncate at a cut-off time tc. A Fourier method will be described to create such time-truncated data. The method leads to a phase-shift migration program without wraparound artifacts.
When the fast Fourier transformation algorithm first came into use people noticed that it could be used for filtering. Transient filtering could be done exactly in the periodic Fourier domain if signals and filters were surrounded by enough zero padding. The same concept applies with migration. If field data and migration hyperbolas are surrounded by enough zeroes in the time- and space-domain then migration can be done in the Fourier domain with no wraparound. The trick is to see how the truncated hyperbolas in Figure 4 can be constructed in the Fourier domain.
To have truncations at time tc,
special point sources must be used.
The deeper the source, the narrower must be its angular aperture.
Take a hyperbola with first arrival
at time t0 to be truncated at some time tc.
The propagation angle ![]() of energy at the cutoff is
given by
of energy at the cutoff is
given by ![]() .So exploding reflectors have their kx-spectrum
truncated at
.So exploding reflectors have their kx-spectrum
truncated at ![]() .A 90
.A 90![]() aperture implies echoes with an infinite time delay.
Here is a sketch of the program.
aperture implies echoes with an infinite time delay.
Here is a sketch of the program.
# Modeling with time truncation at tc ModelFT[model(x,z)] For all
and all kx
. For
..., 0 { For all
{ For all
{ if (
) { sine
if(
sine ) aperture
. else aperture
. } else aperture
.
aperture
Model(kx,z) } } }
FT2D
The above modeling program may be converted to a migration program by running the depth z loop down instead of up and by multiplying the downward continued data by the aperture function. The modifications to the program not only improve the quality of the migration, but the calculation is faster.