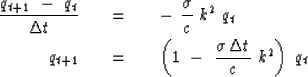Next: Explicit 15 degree migration
Up: INTRODUCTION TO STABILITY
Previous: INTRODUCTION TO STABILITY
Begin with the heat-flow equation and Fourier transform over space.
Thus 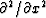 becomes simply - k2,
and
becomes simply - k2,
and
| 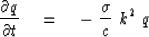 |
(69) |
Finite differencing explicitly over time gives an equation
that is identical in form to the inflation-of-money equation:
| 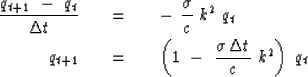 |
(70) |
| (71) |
For stability, the magnitude of qt+1 should be less than or equal to
the magnitude of qt.
This requires the factor in parentheses to have a magnitude less than
or equal to unity.
The dangerous case is when the factor is more negative than -1.
There is instability when 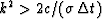 .This means that the high frequencies are diverging with time.
The explicit finite differencing on the time axis has caused disaster
for short wavelengths on the space axis.
Surprisingly, this disaster can be recouped by differencing
the space axis coarsely enough!
The second space derivative in the Fourier transform domain
is
.This means that the high frequencies are diverging with time.
The explicit finite differencing on the time axis has caused disaster
for short wavelengths on the space axis.
Surprisingly, this disaster can be recouped by differencing
the space axis coarsely enough!
The second space derivative in the Fourier transform domain
is 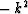 .When the x-axis is discretized it becomes
.When the x-axis is discretized it becomes 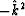 .So, to discretize (69),
(70) and (71), just replace k
by
.So, to discretize (69),
(70) and (71), just replace k
by 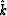 .Equation (68) shows that
.Equation (68) shows that 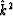 has an upper limit
of
has an upper limit
of 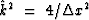 at
the Nyquist frequency
at
the Nyquist frequency 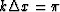 .Finally, the factor in (71) will be
less than unity and there will be stability if
.Finally, the factor in (71) will be
less than unity and there will be stability if
| 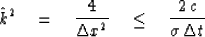 |
(72) |
Evidently instability can be averted by a sufficiently dense sampling
of time compared to space.
Such a solution becomes unbearably costly, however, when the heat
conductivity 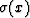 takes on a wide range of values.
For problems in one space dimension, there is an easy escape
in implicit methods.
For problems in higher-dimensional spaces, explicit methods
must be used.
takes on a wide range of values.
For problems in one space dimension, there is an easy escape
in implicit methods.
For problems in higher-dimensional spaces, explicit methods
must be used.





Next: Explicit 15 degree migration
Up: INTRODUCTION TO STABILITY
Previous: INTRODUCTION TO STABILITY
Stanford Exploration Project
10/31/1997
![]() becomes simply - k2,
and
becomes simply - k2,
and