| 3|c| | ||
| 3|c| Forms of stepout operator 2H/v | ||
|---|---|---|
| 3|c| | ||
| ray trace | Fourier | PDE |
Recall the various forms of the stepout operator:
| 3|c| | ||
| 3|c| Forms of stepout operator 2H/v | ||
|---|---|---|
| 3|c| | ||
| ray trace | Fourier | PDE |
Reciprocity suggests that travel time is a symmetrical function of offset;
thus dt/dh vanishes at h = 0.
In that sense it seems appropriate to
apply equation (56) to zero-offset sections.
More precisely,
the ray-trace expression dt/dh strictly applies
only when a single plane wave is present.
Spherical wavefronts are made from the superposition of plane waves.
Then the Fourier interpretation of H is
slightly different and more appropriate.
To set ![]() would be to select a zero frequency component,
a simple integral of a seismic trace.
To set kh = 0 would be to select a
zero spatial-frequency component,
that is, an integration over offset.
Conventional stacking may be defined as integration (or summation)
over offset along a hyperbolic trajectory.
Simply setting kh = 0 is selecting a hyperbolic trajectory
that is flat, namely, the hyperbola of infinite velocity.
Such an integration will receive its major contribution from the top
of the data hyperboloid, where the data events come tangent to the
horizontal line of integration.
(For some historical reason, such a data summation is often called
vertical stack).
Of the total contribution to the integral,
most comes from a zone near the top, before the
stepout equals a half-wavelength.
The width of this zone, which is called a Fresnel zone, is the major factor
contributing to the integral.
The Fresnel zone has been extracted from a field profile in
Figure 29.
would be to select a zero frequency component,
a simple integral of a seismic trace.
To set kh = 0 would be to select a
zero spatial-frequency component,
that is, an integration over offset.
Conventional stacking may be defined as integration (or summation)
over offset along a hyperbolic trajectory.
Simply setting kh = 0 is selecting a hyperbolic trajectory
that is flat, namely, the hyperbola of infinite velocity.
Such an integration will receive its major contribution from the top
of the data hyperboloid, where the data events come tangent to the
horizontal line of integration.
(For some historical reason, such a data summation is often called
vertical stack).
Of the total contribution to the integral,
most comes from a zone near the top, before the
stepout equals a half-wavelength.
The width of this zone, which is called a Fresnel zone, is the major factor
contributing to the integral.
The Fresnel zone has been extracted from a field profile in
Figure 29.
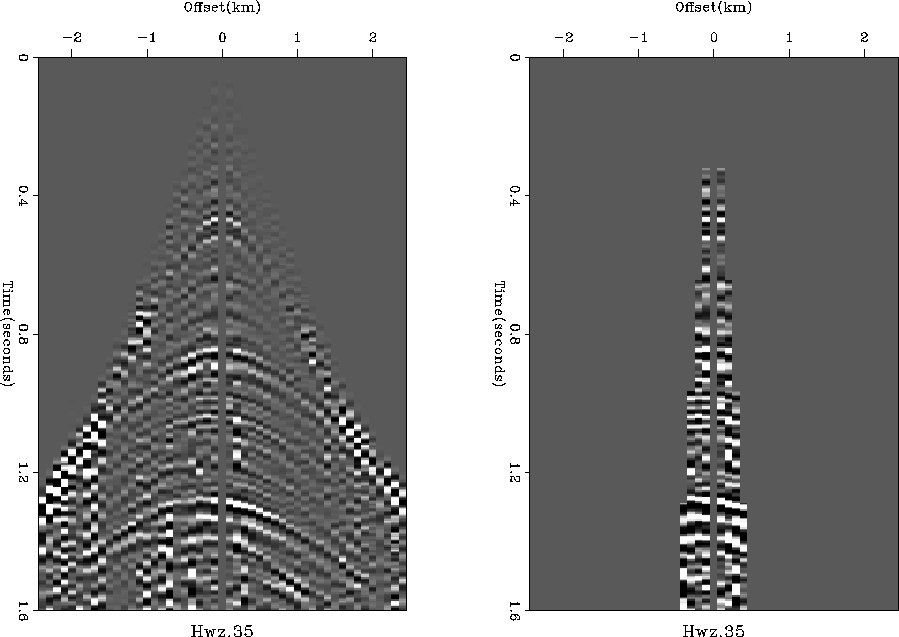 |
The definition of the Fresnel zone involves a frequency.
For practical purposes we may just look at zero crossings.
Examining Figure 29
near one second we see a variety of frequencies.
In the interval between t=1.0 and t=1.1 I see about two
wavelengths of low frequencies and about 5 wavelengths of high frequencies.
The highest frequencies are the main concern,
because they define the limit of seismic resolution.
The higher frequency has about 100 half wavelengths
between time zero and a time of one second.
As a rough generality, this observed value of 100 applies
to all travel times.
That is, at any travel time,
the highest frequency that has meaningful spatial correlations
is often observed to have a half period
of about 1/100 of the total travel time.
We may say that the quality factor Q of the earth's sedimentary crust is
often about 100.
So the angle that we are typically thinking about
is ![]() 8
8![]()
![]() .
.
Theoretically, the main differences between a zero-offset section and a vertical stack are the amplitude and a small phase shift. In practical cases they are unlikely to migrate in a significantly different way. It would be nice if we could find an equation to downward continue data that is stacked at velocities other than infinite velocity.
The partial-differential-equation point of view
of setting H = 0 is identical with the Fourier view when
the velocity is a constant function of the horizontal coordinate;
but otherwise the PDE viewpoint is a slightly more general one.
To be specific,
but not cluttered, equations (54) and(55) can be
expressed in 15![]() retarded, space-domain form.
Thus,
retarded, space-domain form.
Thus,
| |
(62) |
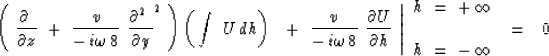 |
(63) |
| |
(64) |
A problem in the development of (64) was that, twice, it was assumed that velocity is independent of offset: first, when the thin-lens term was omitted from (62), and second, when the offset integration operator was interchanged with multiplication by velocity. If the velocity depends on the horizontal x-axis, then it certainly depends on both midpoint and offset. In conclusion: If velocity changes slowly across a Fresnel zone, then setting H = 0 provides a valid equation for downward continuation of vertically stacked data.