While the travel-time curves resulting from a dipping bed are simple,
they are not simple to derive.
Before the derivation, the result will be stated:
for a bed dipping at angle ![]() from the horizontal,
the travel-time curve is
from the horizontal,
the travel-time curve is
| |
(3) |
For a common-midpoint gather at ![]() in (h,t)-space,
equation (3) looks
like
in (h,t)-space,
equation (3) looks
like ![]()
![]() .Thus the common-midpoint gather contains an
exact
hyperbola, regardless of the earth dip angle
.Thus the common-midpoint gather contains an
exact
hyperbola, regardless of the earth dip angle ![]() .The effect of dip is to change the asymptote of the hyperbola,
thus changing the apparent velocity.
The result has great significance in applied work and is
known as Levin's dip correction [1971]:
.The effect of dip is to change the asymptote of the hyperbola,
thus changing the apparent velocity.
The result has great significance in applied work and is
known as Levin's dip correction [1971]:
| |
(4) |
Figure 14 depicts some rays from a common-midpoint gather.
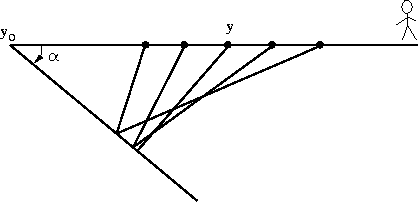 |
Notice that each ray strikes the dipping bed at a different place. So a common-midpoint gather is not a common-depth-point gather. To realize why the reflection point moves on the reflector, recall the basic geometrical fact that an angle bisector in a triangle generally doesn't bisect the opposite side. The reflection point moves up dip with increasing offset.
Finally, equation (3) will be proved. Figure 15 shows the basic geometry along with an ``image'' source on another reflector of twice the dip.
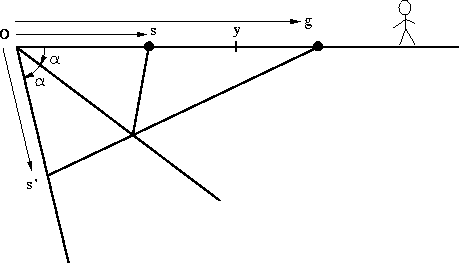 |
For convenience, the bed intercepts the surface at ![]() .The length of the line s' g in Figure 15 is determined by
the trigonometric Law of Cosines to be
.The length of the line s' g in Figure 15 is determined by
the trigonometric Law of Cosines to be
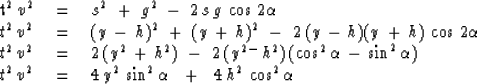 |
||
Another facet of equation (3) is that it describes the constant-offset section. Surprisingly, the travel time of a dipping planar bed becomes curved at nonzero offset--it too becomes hyperbolic.