




Next: THE BULLETPROOFING OF MUIR
Up: IMPEDANCE
Previous: Wide-angle wave extrapolation
By equation (61) and theorem 6, fractional powers of integration
and differentiation are also impedance functions.
Kjartansson [1979] has advocated the fractional power as a
stress-strain law for rocks.
See also Madden [1976].
Classical studies in rock mechanics begin with a stress-strain law
such as
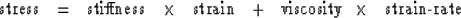
which in the transform domain is
| ![\begin{displaymath}
\rm{stress} \ \ =\ \ [ (- \, i \omega )^0 \ \ \times \ \ \rm...
...mega )^1 \ \
\times \ \ \rm{viscosity} ] \ \times\ \rm{strain}\end{displaymath}](img195.gif) |
(72) |
Experimentally,
the viscoelastic law (72) does a poor job of describing real rocks.
Let us try another mathematical form that is like (72)
in its limiting behavior at high and low viscosity:
| 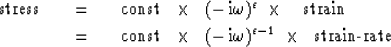 |
(73) |
| (74) |
Here  close to zero gives elastic behavior
and
close to zero gives elastic behavior
and  close to one gives viscous behavior.
The fact that
close to one gives viscous behavior.
The fact that 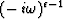 is an impedance
function meshes nicely with the concepts that
(17) stress may be determined from strain history
and strain may be determined from stress history,
and (18) stress times strain-rate is dissipated power.
Kjartansson [1979] points out that
is an impedance
function meshes nicely with the concepts that
(17) stress may be determined from strain history
and strain may be determined from stress history,
and (18) stress times strain-rate is dissipated power.
Kjartansson [1979] points out that 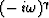 exhibits
the mathematical property called
constant Q,
so that as a stress/strain law for fitting experimental data on rocks,
it is far superior to (72).
To see the constant Q property more clearly,
express
exhibits
the mathematical property called
constant Q,
so that as a stress/strain law for fitting experimental data on rocks,
it is far superior to (72).
To see the constant Q property more clearly,
express 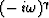 in real and imaginary parts:
in real and imaginary parts:
| ![\begin{eqnarray}
( - \,i \omega )^{\gamma} \ \ \ &=&\ \ \
\vert \omega \vert^{\...
...(\omega )\ \sin \left( {\pi \, \gamma \over 2 }\ \right) \ \right]\end{eqnarray}](img199.gif) |
(75) |
| (76) |
| (77) |
| (78) |
The constant Q property follows from the constant ratio between
the real and imaginary parts of this function.
Q itself is defined by
| 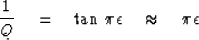 |
(79) |
A pulse with a Q of about 10 is shown in Figure 8.
Qq
Figure 8
The constant Q pulse given
by 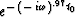 . The frequency axis is represented by a discrete Fourier transform
over 256 points.
Zero time and zero frequency are on the left end
of their respective axes.
. The frequency axis is represented by a discrete Fourier transform
over 256 points.
Zero time and zero frequency are on the left end
of their respective axes.

EXERCISES:
-
Take
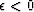 and expand the integration operator for negative
powers of Z.
Explain the sign difference.
and expand the integration operator for negative
powers of Z.
Explain the sign difference.
-
Let
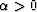 be a real, positive scaling constant,
and let C be a reflectance function.
Without using Muir's rules,
prove that C ' is a reflectance, where
be a real, positive scaling constant,
and let C be a reflectance function.
Without using Muir's rules,
prove that C ' is a reflectance, where
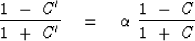
Note that you have proven Muir's first rule.
Muir's third rule can also be proven in an analogous way,
but with much more algebraic detail.
-
The word
isomorphism
means not
only that any impedance R1 , R2 , R ' can be
mapped into a reflectance C1 , C2 , C ' ,
but also that
Muir's three rules will be mapped into
three rules for combining reflectances.
- a.
- What are these three rules?
- b.
- Although C ' = C1 C2 does not turn out
to be one of the three rules, it is obviously true.
Either show that it is a consequence of the three rules
or conclude that it is an independent rule
that can be mapped back into the
domain of the impedances to constitute a fourth rule.
-
Show that the log of the discrete
causal integration operator,
![$ \ln [(1+Z)/(1-Z)] $](img205.gif) , is
one side of the discrete Hilbert transform.
Show that the reflected pulse from a boundary between
two media with the same velocity but slightly
different Q is one side of the Hilbert transform.
, is
one side of the discrete Hilbert transform.
Show that the reflected pulse from a boundary between
two media with the same velocity but slightly
different Q is one side of the Hilbert transform.
-
Consider the fourth-order Taylor expansion for square root in an extrapolation
equation
![\begin{displaymath}
{dP \over dz } \eq i \omega \left[
1 \ -\ {1 \over 2 }\ \lef...
...
{1 \over 8 }\ \left( {vk \over \omega }\ \right)^4 \right] \ P\end{displaymath}](img206.gif)
- a.
- Will this equation be stable for the complex frequency
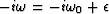 ? Why?
? Why?
- b.
- Consider causal and anticausal time-domain calculations with the equation.
Which, if any, is stable?
-
Consider a material velocity that may depend on the frequency
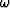 and on
the horizontal x-coordinate as well.
Suppose that, luckily, the velocity can be expressed in the factored
form
and on
the horizontal x-coordinate as well.
Suppose that, luckily, the velocity can be expressed in the factored
form 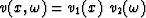 .Obtain a stable 45
.Obtain a stable 45 wave-extrapolation equation.
Hints: try
wave-extrapolation equation.
Hints: try
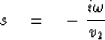
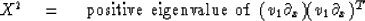
-
Is the Levinson Recursion described in FGDP related
to the rules in this section?
If so, how?
Hint: see Jones and Thron [1980].
-
Show the converse to theorem 4, namely, that if the phase curve
of a causal function does not enclose the origin,
then the inverse is causal.





Next: THE BULLETPROOFING OF MUIR
Up: IMPEDANCE
Previous: Wide-angle wave extrapolation
Stanford Exploration Project
10/31/1997
![]()
![\begin{eqnarray}
( - \,i \omega )^{\gamma} \ \ \ &=&\ \ \
\vert \omega \vert^{\...
...(\omega )\ \sin \left( {\pi \, \gamma \over 2 }\ \right) \ \right]\end{eqnarray}](img199.gif)

![]()
![]()
![]()
![]()