




Next: Nonlinear L.S. conjugate-direction template
Up: MEANS, MEDIANS, PERCENTILES AND
Previous: Weighted L.S. conjugate-direction template
L1 or 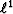 L2 or
L2 or 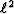 The easiest method of model fitting is linear least squares.
This means minimizing the sums of squares of residuals (
The easiest method of model fitting is linear least squares.
This means minimizing the sums of squares of residuals (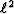 ).
On the other hand, we often encounter huge noises
and it is much safer to minimize
the sums of absolute values of residuals
(
).
On the other hand, we often encounter huge noises
and it is much safer to minimize
the sums of absolute values of residuals
(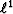 ).
(The problem with
).
(The problem with 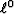 is that there are multiple minima,
so the gradient is not a sensible way to seek the deepest).
is that there are multiple minima,
so the gradient is not a sensible way to seek the deepest).
There exist specialized techniques for handling 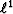 multivariate fitting problems.
They should work better than the simple
iterative reweighting outlined here.
multivariate fitting problems.
They should work better than the simple
iterative reweighting outlined here.
A penalty function that ranges from 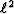 to
to 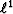 ,depending on the constant
,depending on the constant 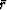 is
is
| 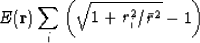 |
(9) |
Where
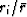 is small, the terms in the sum amount to
is small, the terms in the sum amount to 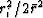 and where
and where
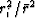 is large, the terms in the sum amount to
is large, the terms in the sum amount to 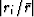 .We define the residual as
.We define the residual as
| 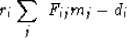 |
(10) |
We will need
| 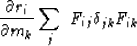 |
(11) |
where we briefly used the notation that 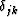 is 1 when
j=k and zero otherwise.
Now,
to let us find the descent direction
is 1 when
j=k and zero otherwise.
Now,
to let us find the descent direction 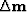 ,we will compute
the k-th component gk of the gradient
,we will compute
the k-th component gk of the gradient 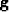 .We have
.We have
| 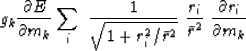 |
(12) |
| 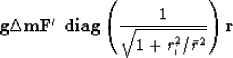 |
(13) |
where we have use the notation 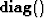 to designate
a diagonal matrix with its argument distributed along the diagonal.
to designate
a diagonal matrix with its argument distributed along the diagonal.
Continuing, we notice that the new weighting of residuals
has nothing to do with the linear relation between model perturbation
and residual perturbation;
that is,
we retain the familiar relations,
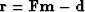 and
and
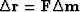 .
.
In practice we have the question of how to choose 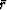 .I suggest that
.I suggest that 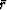 be proportional to
be proportional to
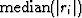 or some other percentile.
or some other percentile.





Next: Nonlinear L.S. conjugate-direction template
Up: MEANS, MEDIANS, PERCENTILES AND
Previous: Weighted L.S. conjugate-direction template
Stanford Exploration Project
4/27/2004
![]() multivariate fitting problems.
They should work better than the simple
iterative reweighting outlined here.
multivariate fitting problems.
They should work better than the simple
iterative reweighting outlined here.
![]() to
to ![]() ,depending on the constant
,depending on the constant ![]() is
is
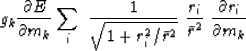
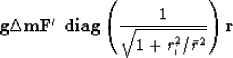
![]() and
and
![]() .
.![]() .I suggest that
.I suggest that ![]() be proportional to
be proportional to
![]() or some other percentile.
or some other percentile.