![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
There we identified defective data by its lack
of continuity. We used the fitting equations
.
There we identified defective data by its lack
of continuity. We used the fitting equations
We can use the same technique to throw out fitting equations
from defective data that we use for missing data.
Recall the theory and discussion leading up to
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
There we identified defective data by its lack
of continuity. We used the fitting equations
.
There we identified defective data by its lack
of continuity. We used the fitting equations
![]() where the weights wi were chosen
to be approximately the inverse
to the residual (yi+1 -2yi + yi-1) itself.
where the weights wi were chosen
to be approximately the inverse
to the residual (yi+1 -2yi + yi-1) itself.
Here we will first use the second derivative
(Laplacian in 1-D) to throw out bad points,
while we determine the PEF.
Having the PEF, we use it to fill in the missing data.
pefestestimate PEF in 1-D avoiding bad data
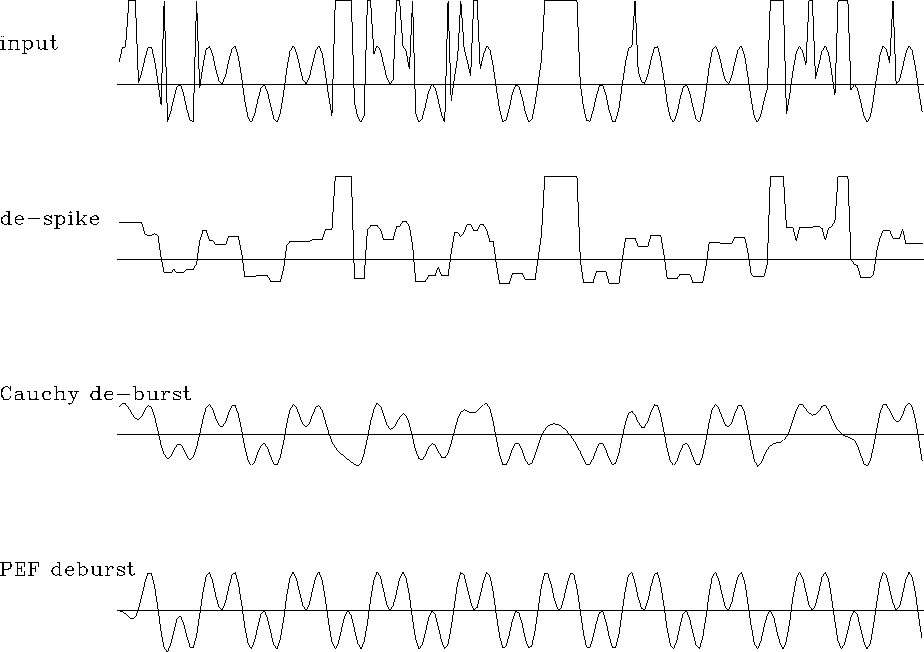
The result of this ``PEF-deburst'' processing
is shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
 |
Given the PEF that comes out of pefest1()![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) , subroutine
fixbad1() below convolves it with the data and looks for
anomalous large outputs. For each that is found, the input data is
declared defective and set to zero. Then subroutine mis1()
, subroutine
fixbad1() below convolves it with the data and looks for
anomalous large outputs. For each that is found, the input data is
declared defective and set to zero. Then subroutine mis1()
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) is invoked to replace the zeroed values by
reasonable ones.
fixbadrestore damaged data
is invoked to replace the zeroed values by
reasonable ones.
fixbadrestore damaged data