




Next: Looping over input space
Up: Moveout, velocity, and stacking
Previous: Moveout, velocity, and stacking
Here we see how general principles of linear operators
are exemplified by linear interpolation.
Because the subject matter is so simple and intuitive,
it is ideal to exemplify abstract mathematical concepts
that apply to all linear operators.
Let an integer k range along a survey line,
and let data values xk be packed into a vector  .(Each data point xk could also be a seismogram.)
Next we resample the data more densely,
say from 4 to 6 points.
For illustration, I follow a crude
nearest-neighbor interpolation
.(Each data point xk could also be a seismogram.)
Next we resample the data more densely,
say from 4 to 6 points.
For illustration, I follow a crude
nearest-neighbor interpolation
scheme by sprinkling ones along the diagonal of a rectangular matrix
that is
| 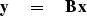 |
(1) |
where
| ![\begin{displaymath}
\left[
\begin{array}
{c}
y_1 \\
y_2 \\ y_3 \\ y_4 \\...
...{array}
{c}
x_1 \\
x_2 \\ x_3 \\ x_4
\end{array} \right]\end{displaymath}](img3.gif) |
(2) |
The interpolated data is simply
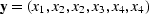 .The matrix multiplication (2)
would not be done in practice.
Instead there would be a loop running over the space of the
outputs
.The matrix multiplication (2)
would not be done in practice.
Instead there would be a loop running over the space of the
outputs 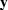 that picked up values from the input.
that picked up values from the input.





Next: Looping over input space
Up: Moveout, velocity, and stacking
Previous: Moveout, velocity, and stacking
Stanford Exploration Project
12/26/2000
![]() .(Each data point xk could also be a seismogram.)
Next we resample the data more densely,
say from 4 to 6 points.
For illustration, I follow a crude
nearest-neighbor interpolation
.(Each data point xk could also be a seismogram.)
Next we resample the data more densely,
say from 4 to 6 points.
For illustration, I follow a crude
nearest-neighbor interpolation
![\begin{displaymath}
\left[
\begin{array}
{c}
y_1 \\
y_2 \\ y_3 \\ y_4 \\...
...{array}
{c}
x_1 \\
x_2 \\ x_3 \\ x_4
\end{array} \right]\end{displaymath}](img3.gif)