The 45![]() diffraction equation differs from the 15
diffraction equation differs from the 15![]() equation
by the inclusion of a
equation
by the inclusion of a ![]() -derivative.
Luckily this derivative fits on the six-point differencing star
-derivative.
Luckily this derivative fits on the six-point differencing star
| -1 | 2 |
| 1 | -2 |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) yields wider angles.
yields wider angles.
|
Mfortyfive90
Figure 10 Figure 2 including the 45 | 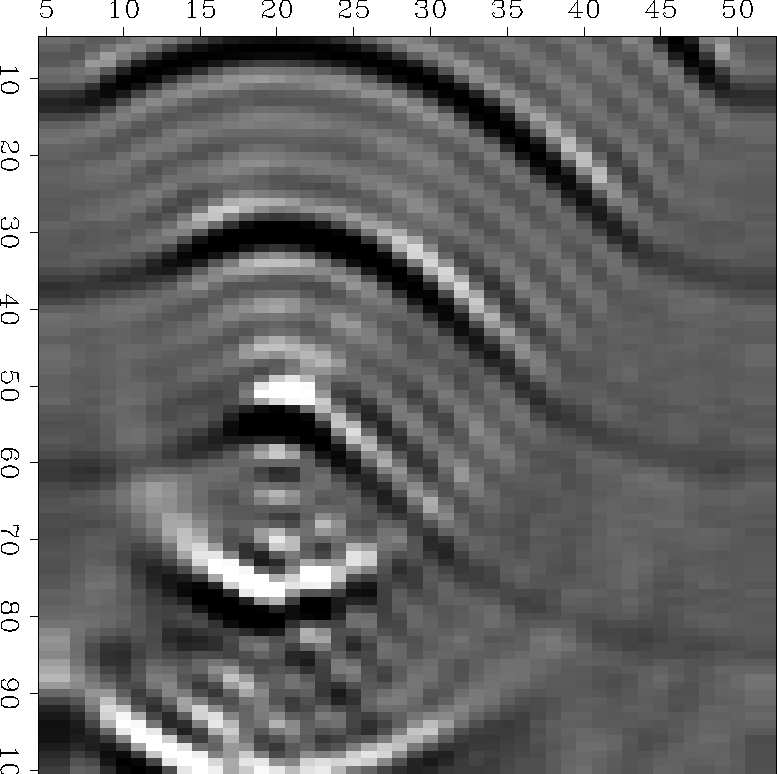 |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
|
Mhi45b90
Figure 11 The accuracy of the x-derivative may be improved by a technique that is analyzed in IEI p 262-265. Briefly, instead of representing | 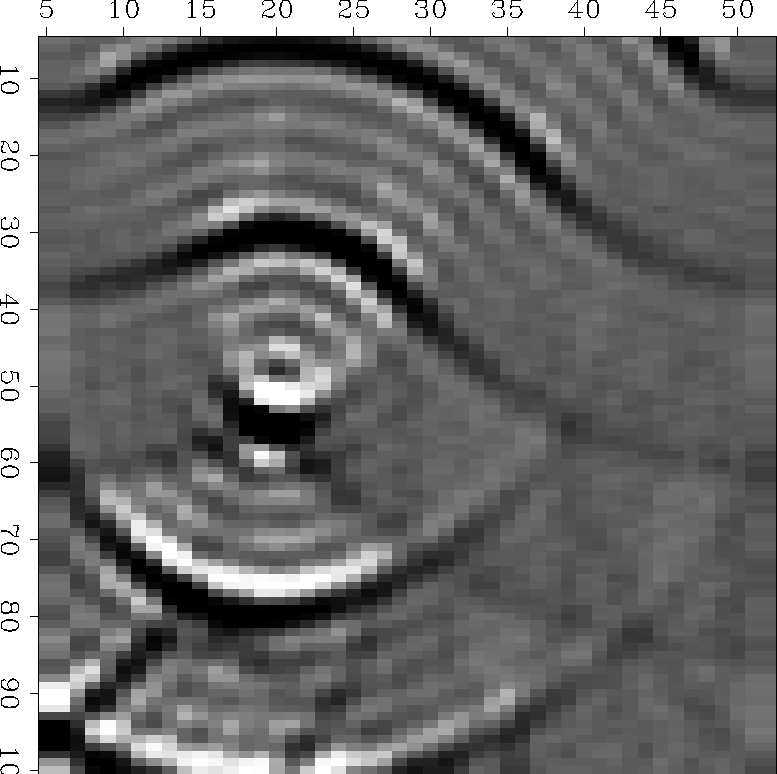 |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
Theory predicts that in two dimensions,
waves going through a focus
suffer a 90![]() phase shift.
You should be able to notice that a symmetrical waveform
is incident on the focus, but an antisymmetrical waveform emerges.
This is easily seen in Figure 11.
phase shift.
You should be able to notice that a symmetrical waveform
is incident on the focus, but an antisymmetrical waveform emerges.
This is easily seen in Figure 11.
In migrations, waves go just to a focus, not through it.
So the migration impulse response in two dimensions
carries a 45![]() phase shift.
Even though real life is three dimensional,
the two-dimensional response is appropriate
for migrating seismic lines where focusing
is presumed to arise from cylindrical, not spherical, reflectors.
phase shift.
Even though real life is three dimensional,
the two-dimensional response is appropriate
for migrating seismic lines where focusing
is presumed to arise from cylindrical, not spherical, reflectors.
1