Anisotropic model building with rock physics modeling
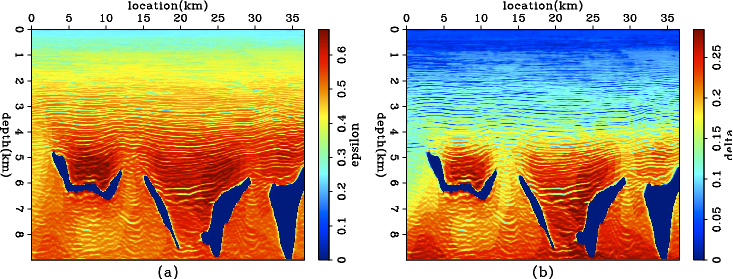
- Anisotropic model building using surface seismic data is a well-known under-determined and nonlinear problem. Inversion lost direction in the null space and ended up with ambiguous models. Albert Tarantola taught us that adding a model covariance can regularize the inversion. However, how to build a covariance matrix remains a mystery. In the current studies, we build the anisotropic prior model using deterministic and stochastic rock physics modeling for shale anisotropy. An ensemble of rock physics models are generated by sample the input parameters in a certain region, which can be significantly narrowed down using well log measurements. The lithological inversion results of a previous seismic processing workflow can also be used as the input of the rock physics modeling.
- Yunyue Li, Dave Nichols, & Gary Mavko, 2013, SEP Report - 149; SEP Report - 150
- [Report]
Image-guided WEMVA for azimuthal anisotropy
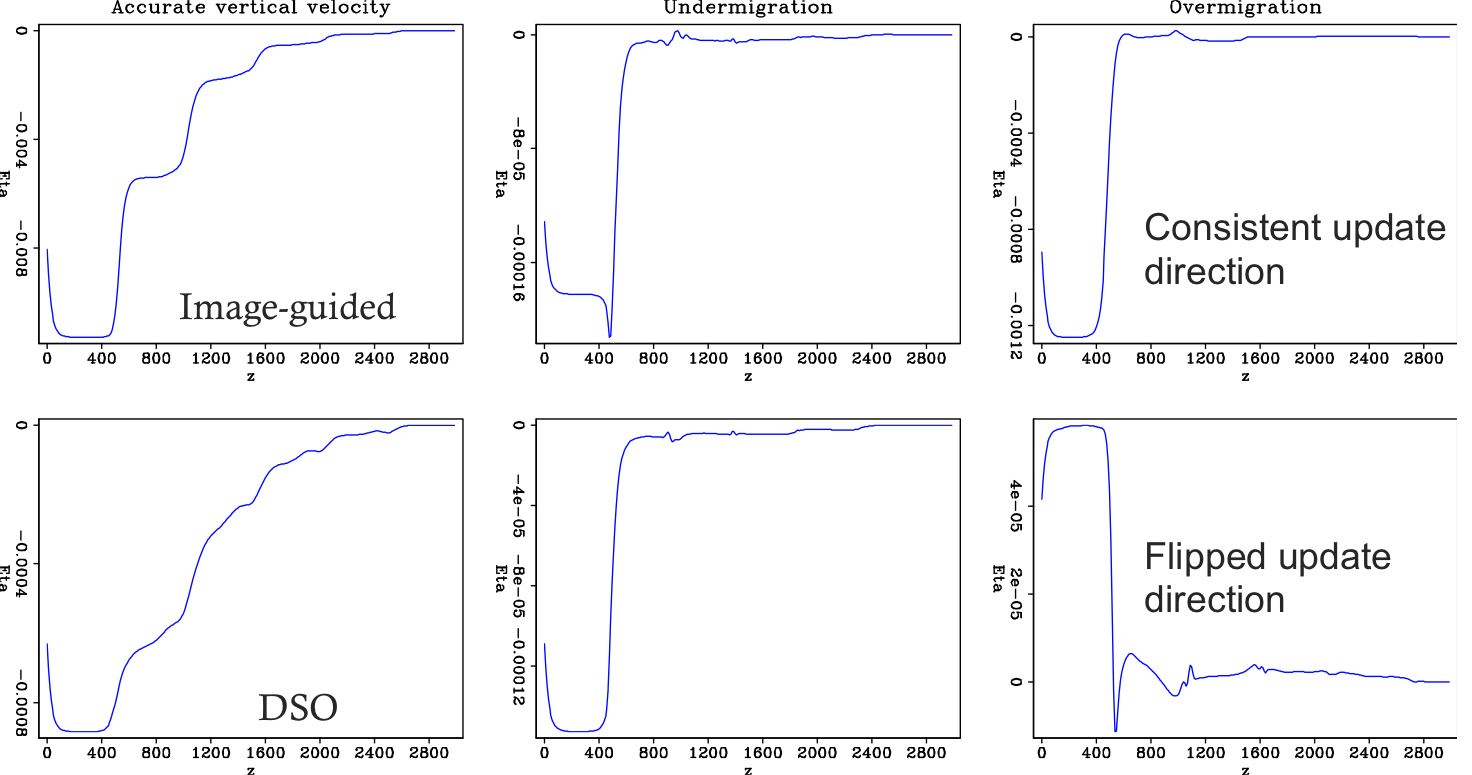
- Often times we have multiple images of the same subsurface. This redundancy has been utilized in many model building processes. In azimuthal anisotropy, traditional processing on individual azimuths usually yields images with inconsistent depths. In this study, we propose to use an image obtained from one azimuth to constrain the image-space velocity analysis on other azimuths. This method directly tackles the differences in anisotropic parameters among different azimuths. By keeping the vertical velocity constant across the azimuths, we separate the kinematic effects due to the anisotropic parameters from those due to the velocity error.
- Yunyue Li, 2013, 83nd Annual International Meeting, Society of Exploration Geophysicists.
- [Expanded Abstract]
Post-propagation filtering for temporal dispersion
- Numerical dispersion in computer-based modeling will produce constructive events which do not exist in the field data. It is interesting that the temporal dispersion is independent with the propagation speed and the spatial grid, but purely determined by the time stepping and the propagation time. Taking advantage of this, we design post-propagation filters to remove the temporal dispersion effects at a very small cost.
- Yunyue Li, Mandy Wong and Robert Clapp, 2013, SEP Report - 150.
- [Report]
WEMVA for anisotropic models

- The reason why I like image-space model building methods is that they produce better models and better images at the same time. By including anisotropy, we estimate the Earth property one step closer to the true Earth. Hence the data collected from the Earth experiments can be better explained. The inverted models can also help seismic interpretation and lithological inversion.
- Yunyue Li and Biondo Biondi, 2012, SEP Report - 147, 148.
- [Extended Abstract]
Robust inversion for sparse models
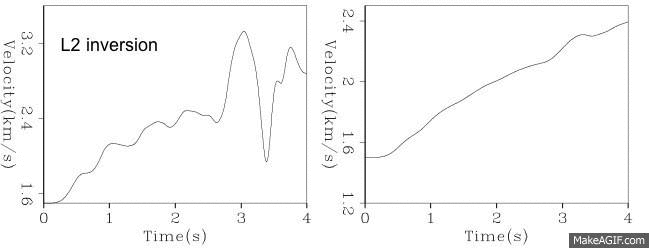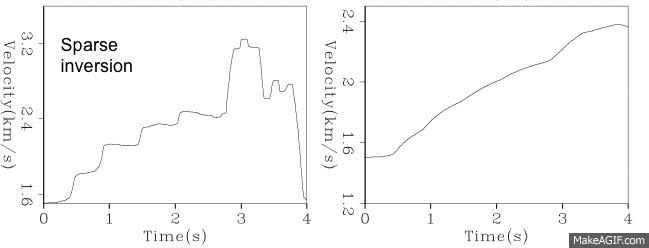
- In the practice of exploration geophysics, we find that a hyperbolic penalty function which has both the characteristics of L1 and L2 penalty functions is preferential. We also find that often times the distribution of the data residuals is different from that of the model residuals. We achieve robustness by using L1 characteristics in the data fitting. We achieve sparseness by using L1 characteristics in the model regularization.
- Yunyue Li, Yang Zhang and Jon Claerbout, 2012, Geophysics.
- [Geophysics paper]