




Next: General approach to waveform
Up: Review of Frequency-domain waveform
Previous: Conjugate Gradient Definition
After computing the (conjugate) gradient vector, one must calculate the step length, 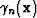 , used to update model parameters (equation 5). This computation is not straightforward because the acoustic wave equation is non-linear in model parameters
, used to update model parameters (equation 5). This computation is not straightforward because the acoustic wave equation is non-linear in model parameters 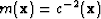 and the Frechét derivatives are never explicitly calculated. One approach is to use a linear approximation technique based on perturbation methods Mora (1987). This involves calculating an approximate Frechét derivative,
and the Frechét derivatives are never explicitly calculated. One approach is to use a linear approximation technique based on perturbation methods Mora (1987). This involves calculating an approximate Frechét derivative, 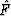 , by performing an additional forward modeling using a set of model parameters perturbed by a scaled version of the computed conjugate gradient (i.e.
, by performing an additional forward modeling using a set of model parameters perturbed by a scaled version of the computed conjugate gradient (i.e. 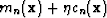 ) and comparing the result with the initial forward modeled data. This is summarized notationally as
) and comparing the result with the initial forward modeled data. This is summarized notationally as
| 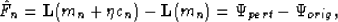 |
(12) |
where 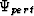 and
and 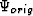 are the perturbed and original wavefields, respectively. Perturbation scaling factor
are the perturbed and original wavefields, respectively. Perturbation scaling factor  is constrained to be within
is constrained to be within 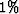 of the current model parameter values. The step-length is then given by Mora (1987)
of the current model parameter values. The step-length is then given by Mora (1987)
| 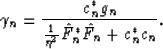 |
(13) |
Again, the step-length in equation 13 is equal to that in Mora (1987) where covariance matrices are represented by identity operators.





Next: General approach to waveform
Up: Review of Frequency-domain waveform
Previous: Conjugate Gradient Definition
Stanford Exploration Project
1/16/2007