




Next: About this document ...
Up: Oddysee of a project
Previous: Appendix: Zoeppritz
I designed a small object-oriented finite difference
library. The idea was to have a set of basic operators that I can combine
to more complex ones. In the case of the wave equation, I intended to
build the operator from operators that implement the equation of state,
motion, and viscosity.
I gave up on this approach,
when I could not find stable parameters for the explicit formulation of
the scalar acoustic wave propagation in viscous material.
Building the
wave equation from basic operators lead to a rather complex condition
for stability, as I will show below.
I did not expect
the stability analysis for the compounded wave operator
to be more complex than
the analysis for the standard implementation.
Anyway, here is what I found until I abandoned the project:
The derivation of the acoustic wave equation is based on the
combination of three equations that have physical meaning by themselves.
The continuity equation describes the excess mass flow
due to the divergence of 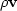 , the local density and
material velocity:
, the local density and
material velocity:
| 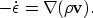 |
(46) |
(Obviously, an excess in mass flow changes the density: the
density is defined as time average, so that
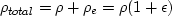 .)
The equation of state relates the change in excess pressure
.)
The equation of state relates the change in excess pressure  to a change in excess density
to a change in excess density  .
For elastic behavior, the equation is simply
Hook's law
.
For elastic behavior, the equation is simply
Hook's law  .
The elastic description of Hook's law is a good approximation
for many materials and situations.
However, the approximation has obvious shortcomings,
e.g. the response to pressure is instantaneous, reversible, and without
friction loss. An improvement, albeit still an idealized approximation,
is the viscous equation of state
.
The elastic description of Hook's law is a good approximation
for many materials and situations.
However, the approximation has obvious shortcomings,
e.g. the response to pressure is instantaneous, reversible, and without
friction loss. An improvement, albeit still an idealized approximation,
is the viscous equation of state
| 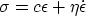 |
(47) |
which accounts for a time delay in change of excess density.
Finally the equation of motion encapsulates Newton's
second law 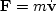 .
In our formulation it relates a change in material velocity to the
change in excess pressure,
.
In our formulation it relates a change in material velocity to the
change in excess pressure,
| 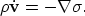 |
(48) |
The three equations do constitute the wave equation.
The substitution of 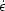 in the equation of state
by the corresponding expression
in the equation of continuity 48, yields
in the equation of state
by the corresponding expression
in the equation of continuity 48, yields
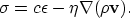
The partial time derivative of the expression is
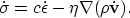
where I interchanged the order of differentiation assuming well-behaved
solutions.
Substitution of 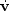 by an expression derived from the
equation of motion 50 yields
by an expression derived from the
equation of motion 50 yields
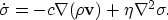
Finally,
the partial time derivative of this expression
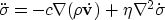
and the divergence of the equation of motion 50
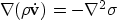
allow us to eliminate the velocity term and yield the viscous
wave equation for the material's pressure
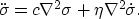
Instead of implementing the wave equation directly,
I decided to implement a system of three partial differential
equations of which each equation has its own meaning and application.
The elastic part of equation of state 49 and
the continuity equation 48
combine to
| 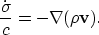 |
(49) |
The viscous part of the equation of state
is formulated as an independent heat equation
| 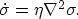 |
(50) |
The equation of motion stays unchanged![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) .
.
The discrete version of
the combined state and continuity equation 51 is
![\begin{displaymath}
\sigma_{t+1}^{x,y} = \sigma_t^{x,y} - \frac{c \rho \Delta t}...
...lta x}
[(u_t^{x,y} - u_t^{x-1,y}) + (v_t^{x,y} - v_t^{x,y-1})]\end{displaymath}](img159.gif)
where
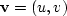 are the components of the velocity vector in two dimensions,
the superscript indicates the spatial sample,
the subscript indicates the temporal sample, and
are the components of the velocity vector in two dimensions,
the superscript indicates the spatial sample,
the subscript indicates the temporal sample, and
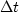 and
and 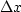 are the respective discrete increments between
samples.
In two dimensions,
the equation of motion 50 has two components
Finally, the discretization of the heat equation 52
yields
are the respective discrete increments between
samples.
In two dimensions,
the equation of motion 50 has two components
Finally, the discretization of the heat equation 52
yields
![\begin{displaymath}
\sigma_{t+1}^{x,y} = \sigma_t^{x,y} - \frac{\eta \Delta t}{\...
...) +
(\sigma_t^{x,y-1} - 2 \sigma_t^{x,y} + \sigma_t^{x,y+1})].\end{displaymath}](img162.gif)
frog
Figure 9
Snapshots of the viscous elastic wave equation simulator.
The simulator is instable.





I programmed the three equations, and
Figure 9 shows snapshots for a
point source and progressing time.
The later frames show the computation to be instable, a standard problem
with explicit finite difference schemes.
I first tried to guess parameters 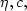 and
and 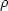 for which the
computation would be stable. I mostly increased the viscosity to
counteract the exponential amplitude growth by exponential amplitude
reduction. When I failed to find appropriate values, I decided to
estimate the stability limits of the parameters by careful analysis
of the Courant-Levy criteria.
for which the
computation would be stable. I mostly increased the viscosity to
counteract the exponential amplitude growth by exponential amplitude
reduction. When I failed to find appropriate values, I decided to
estimate the stability limits of the parameters by careful analysis
of the Courant-Levy criteria.
The eigenmodes of the discrete equation system are
![\begin{displaymath}
\left[
\begin{array}
{c}
\sigma_t^{x,y} \\ u_t^{x,y} \\ v_t^...
...t[
\begin{array}
{c}
\sigma_0 \\ u_0 \\ v_0 \end{array}\right].\end{displaymath}](img164.gif)
Substitution of the right hand side in the system of difference equations
(now written as a matrix operator) yields
![\begin{displaymath}
\left[
\begin{array}
{c}
0 \\ 0 \\ 0\end{array}\right]
=
\le...
...ft[
\begin{array}
{c}
\sigma_0 \\ u_0 \\ v_0 \end{array}\right]\end{displaymath}](img165.gif)
where
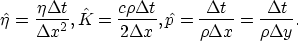
To find the stability limit, I need to find parameters
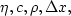 and
and 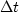 so that all the eigenvalues
of the propagation matrix are smaller than 1.
This is equivalent with ensuring that the values of
so that all the eigenvalues
of the propagation matrix are smaller than 1.
This is equivalent with ensuring that the values of 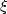 for
which the determinant of the matrix is zero are all smaller than 1.
The limit has to hold for all wave numbers kx and ky.
The determinant is a third order polynomial in
for
which the determinant of the matrix is zero are all smaller than 1.
The limit has to hold for all wave numbers kx and ky.
The determinant is a third order polynomial in 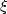 and the
estimation of the upper limit requires very careful accounting of the sign of
all the exponential expressions.
When I first investigated the problem, I was stumped.
But now I realize that I can find the boundaries by computing the
zeroes of the corresponding derivatives and by checking the particular
boundary values.
The computation is tiresome but feasible.
I, however, had already moved on and implemented the simpler acoustic
wave equation.
and the
estimation of the upper limit requires very careful accounting of the sign of
all the exponential expressions.
When I first investigated the problem, I was stumped.
But now I realize that I can find the boundaries by computing the
zeroes of the corresponding derivatives and by checking the particular
boundary values.
The computation is tiresome but feasible.
I, however, had already moved on and implemented the simpler acoustic
wave equation.





Next: About this document ...
Up: Oddysee of a project
Previous: Appendix: Zoeppritz
Stanford Exploration Project
3/9/1999
![]() , the local density and
material velocity:
, the local density and
material velocity:
![]() in the equation of state
by the corresponding expression
in the equation of continuity 48, yields
in the equation of state
by the corresponding expression
in the equation of continuity 48, yields
![]()
![]()
![]()
![]()
![]()
![]()
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) .
.
![]()
![\begin{eqnarraystar}
u_{t+1}^{x,y} &=& u_t^{x,y} - \frac{\Delta t}{\rho \Delta x...
...Delta t}{\rho \Delta x}
[\sigma_t^{x,y+1} - \sigma_t^{x,y}].\end{eqnarraystar}](img161.gif)
![]()

![]() and
and ![]() for which the
computation would be stable. I mostly increased the viscosity to
counteract the exponential amplitude growth by exponential amplitude
reduction. When I failed to find appropriate values, I decided to
estimate the stability limits of the parameters by careful analysis
of the Courant-Levy criteria.
for which the
computation would be stable. I mostly increased the viscosity to
counteract the exponential amplitude growth by exponential amplitude
reduction. When I failed to find appropriate values, I decided to
estimate the stability limits of the parameters by careful analysis
of the Courant-Levy criteria.
![\begin{displaymath}
\left[
\begin{array}
{c}
\sigma_t^{x,y} \\ u_t^{x,y} \\ v_t^...
...t[
\begin{array}
{c}
\sigma_0 \\ u_0 \\ v_0 \end{array}\right].\end{displaymath}](img164.gif)
![\begin{displaymath}
\left[
\begin{array}
{c}
0 \\ 0 \\ 0\end{array}\right]
=
\le...
...ft[
\begin{array}
{c}
\sigma_0 \\ u_0 \\ v_0 \end{array}\right]\end{displaymath}](img165.gif)
![]()