Next: Results
Up: Standard edge detection
Previous: Processing and display parameters
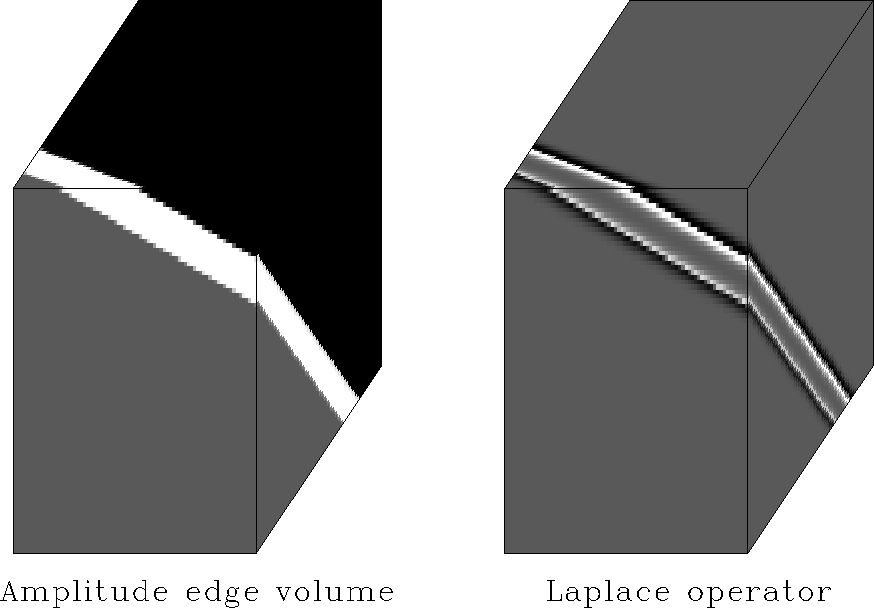
In Figure 18,
a Laplace operator transforms the amplitude edges
in the image cube on the left
to zero crossings of a bipolar wavelet
in the image cube on the right.
Given an image volume 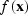 ,
the Laplace operator
,
the Laplace operator
zeroes the amplitude where f is constant.
Analogous to the gradient magnitude operator case,
a Laplace operator is conveniently approximated
by its finite difference approximations, such as those shown in
Table 3.
In general,
the masks vary in their moments and consequently in their
isotropy, robustness and resolving power.
In this chapter,
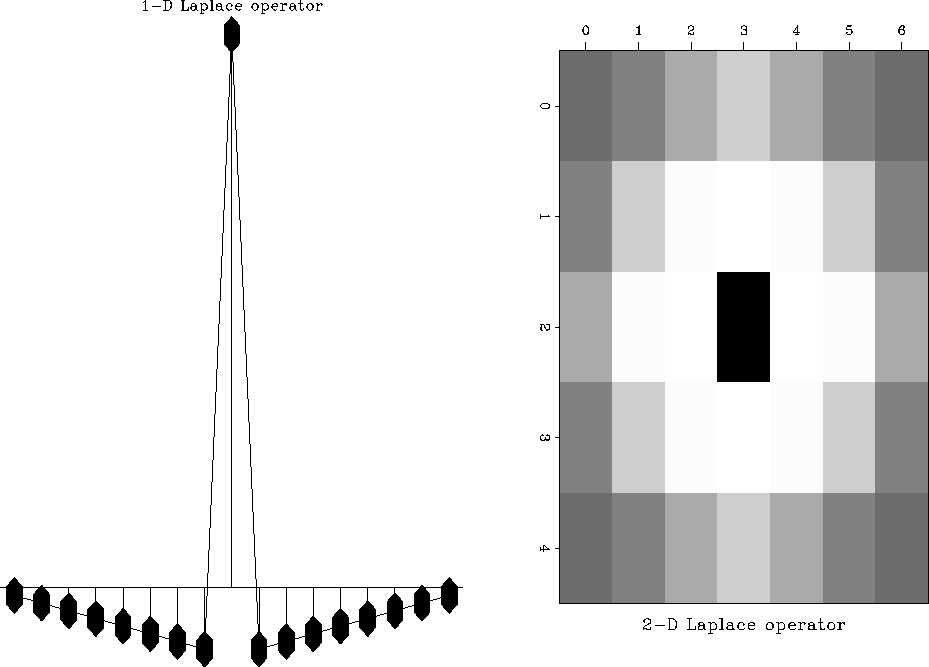
I use a three-dimensional version of
the one-dimensional and two-dimensional Laplace filters
of Figure 19.
consFoltLap
Figure 18
Laplace operator applied to constant amplitude image.
The output of the Laplace operator on the right delineates
the edges successfully.
Edges are indicated by the zero-crossing (grey) of a bipolar wavelet.
Constant input regions result in zero output values (grey).





lapGeneral
Figure 19
Generalized Laplace operator.
The one-dimensional filter on the left is constructed by
subtracting a wide and a narrow triangle of equal area.
Similarly,
the two-dimensional filter on the right is constructed by
subtracting a wide and a narrow pyramid of equal volume.





Table 3:
Finite-difference approximations of the 2-D Laplace operator.
|
-1 |
|
|
| -1 |
4 |
-1 |
|
| |
-1 |
0
$ |
|
| -1 |
8 |
-1 |
|
| -1 |
-1 |
-1
$ |
|
| -2 |
4 |
-2 |
|
| 1 |
-2 |
1
$ |
|
| -1 |
-1 |
-1 |
-1 |
| -1 |
-1 |
24 |
-1 |
| -1 |
-1 |
-1 |
-1 |
| -1 |
-1 |
-1 |
-1 |
The finite-difference representations of Table 3
approximate
a generalized Laplace operator
that combines the nabla operator
with a pre-smoothing by a Gaussian:
where controls the width of the Gaussian kernel.
In the Fourier domain,
the generalized Laplace operator (5)
is
The factor (u2 + v2) is the Fourier transform of the nabla operator;
the exponential is the transform of the Gaussian low-pass filter.





Next: Results
Up: Standard edge detection
Previous: Processing and display parameters
Stanford Exploration Project
3/8/1999
![]() ,
the Laplace operator
,
the Laplace operator