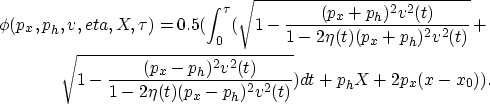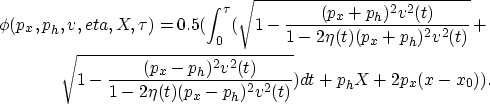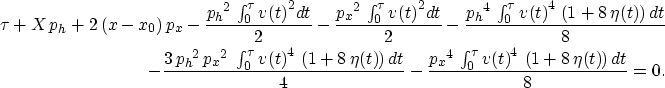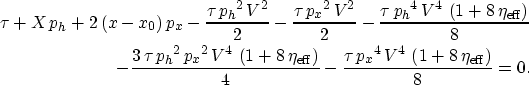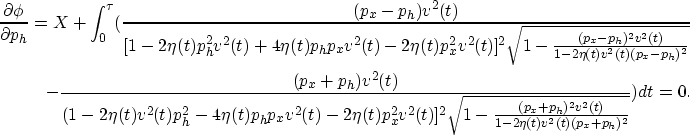Vertically heterogenous media

The same approach used in homogeneous media is followed here. Starting with the phase of exponential for VTI v(z) media which is given by

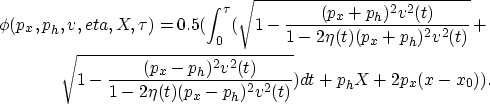$$\begin{eqnarray} \phi(p_x,p_h,v,eta,X,\tau) = 0.5 (\int_0^{\tau} (\sqrt{1-\frac... ...(t)}{1-2 \eta(t) (p_x-p_h)^2 v^2(t)}}) dt + p_h X +2 p_x (x-x_0)).\end{eqnarray}$$ (26)

Using Taylor series, I expand equation (26) around p_h=0 and p_x=0, which corresponds to small offsets and dips. In the Taylor series expansion of equation (26), I drop terms beyond the quartic power in p_h and p_x. Thus,

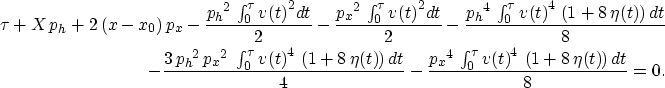$$\begin{eqnarray} \tau + X\,{p_h} + 2\,(x-x_0)\,{p_x} - {\frac{{{{p_h}}^2}\, \i... ...0^{\tau} {{v(t)}^4}\, \left( 1 + 8\,{\eta(t)} \right) dt }{8}}=0.\end{eqnarray}$$ (27)

As mentioned earlier, the analytical homogeneous-medium equations can be used to calculate traveltimes in vertically inhomogeneous media, granted that the medium parameters are replaced by their equivalent averages in v(z) media. Thus, equation (20) becomes  

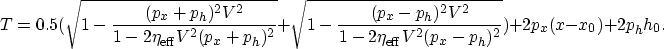$$T = 0.5(\sqrt{1-\frac{(p_x+p_h)^2 V^2}{1-2 \eta_{\rm eff} V^... ...{1-2 \eta_{\rm eff} V^2 (p_x-p_h)^2}})+2 p_x (x-x_0)+2 p_h h_0.$$ (28)

The Taylor series expansion of equation (28) around p_h=0 and p_x=0, with terms beyond the quartic power in p_h and p_x dropped, yields

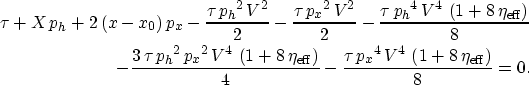$$\begin{eqnarray} \tau + X\,{p_h} + 2\,(x-x_0)\,{p_x} - {\frac{\tau \,{{{p_h}}^... ...}\,{{{V}}^4}\, \left( 1 + 8\,{{\eta }_{\rm eff}} \right) }{8}}=0.\end{eqnarray}$$ (29)

Matching coefficients of terms with the same power in p_x and p_h in equations (27) and (29) provides us with two key relations:  

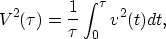$$V^2(\tau)=\frac{1}{\tau} \int_0^{\tau} v^2(t) dt,$$ (30)

and  

$$\eta_{{\rm eff}}(\tau)=\frac{1}{8} \{ \frac{1}{t_0 V^4(\tau)} \int_0^{\tau} v^4(t)[1+8 \eta(t)] dt -1\}.$$ (31)

The stationary points (p_h and p_x), in vertically inhomogeneous media, satisfy

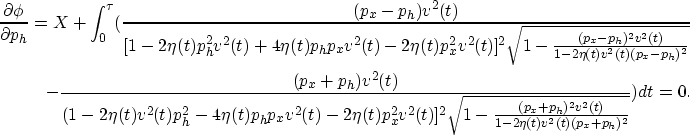$$\begin{eqnarray} \frac{\partial \phi}{\partial p_h} = X+\int_0^{\tau} (\frac{(p_... ...rac{(p_x+p_h)^2 v^2(t)}{1-2 \eta(t) v^2(t) (p_x+p_h)^2}}}) dt =0.\end{eqnarray}$$ (32)

with solutions best solved numerically. Again by expanding this equation in powers of p_x and p_h and matching its coefficients with the coefficients of an equivalent expansion of the effective equation, we obtain equations (30) and (31) again.

In summary, equations (30) and (31) provide us with the equivalent relations necessary to use the offset-midpoint traveltime equation for homogeneous VTI media in v(z) media.

C