




Next: Suppressing wraparound artifacts of
Up: Fourier approach
Previous: Fourier approach
The first problem is the loss of information in the transform to the
t2 grid. As illustrated in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , the shallow part of
the data gets severely compressed in the t2 grid. The amount of
compression can lead to inadequate sampling, and as a result, aliasing
artifacts in the frequency domain. Moreover, it can be difficult to
recover from the loss of information in the transformed domain when
transforming back into the original grid. A partial remedy for this
problem is to increase the grid size in the t2 domain. The top plots
in Figure
, the shallow part of
the data gets severely compressed in the t2 grid. The amount of
compression can lead to inadequate sampling, and as a result, aliasing
artifacts in the frequency domain. Moreover, it can be difficult to
recover from the loss of information in the transformed domain when
transforming back into the original grid. A partial remedy for this
problem is to increase the grid size in the t2 domain. The top plots
in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show the result of back transformation to
the t grid and the difference between this result and the original
model (plotted on the same scale). We can see a noticeable loss of
information in the upper (shallow) part of the data, caused by
undersampling. The bottom plots in Figure
show the result of back transformation to
the t grid and the difference between this result and the original
model (plotted on the same scale). We can see a noticeable loss of
information in the upper (shallow) part of the data, caused by
undersampling. The bottom plots in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) correspond
to increasing the grid size by a factor of three. Some of the
artifacts have been suppressed, at the expense of dealing with a
larger grid.
correspond
to increasing the grid size by a factor of three. Some of the
artifacts have been suppressed, at the expense of dealing with a
larger grid.
fft-inv
Figure 4 The left plots show the reconstruction of the original data
after transforming back from the t2 grid to the original t
grid. The right plots show the difference with the original model.
Top: using the original grid size (Nt = 200). Bottom: increasing
the grid size by a factor of three.





To perform an accurate transform of the grid, I adopted the following
method, inspired by (). Let 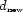 denote the data on the new grid and
denote the data on the new grid and 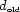 be the data on the old grid. If L is the interpolation operator,
defined on the new grid, then the optimal least-square transformation
is
be the data on the old grid. If L is the interpolation operator,
defined on the new grid, then the optimal least-square transformation
is
| 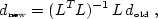 |
(89) |
where LT denotes the adjoint interpolation operator. The operator
(LT L)-1 provides a proper scaling of the result. If we use
simple linear interpolation for the L operator, then LT L is a
tridiagonal matrix, which can be easily inverted (in 8 N
operations). If some parts in 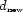 are not fully
constrained, then the tridiagonal matrix is not invertible. To obtain
a solution in this case, we can include a regularization operator D
in (
are not fully
constrained, then the tridiagonal matrix is not invertible. To obtain
a solution in this case, we can include a regularization operator D
in (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), as follows:
), as follows:
| 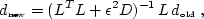 |
(90) |
A convenient choice for D is a second derivative operator,
represented with the second-order finite-difference approximation.
This operator allows the selection of the smoothest possible function
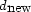 while preserving the efficient tridiagonal structure
of
while preserving the efficient tridiagonal structure
of 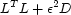 . In this problem, the parameter
. In this problem, the parameter  can be chosen as small as possible, as long as it prevents the
inversion from getting unstable.
can be chosen as small as possible, as long as it prevents the
inversion from getting unstable.





Next: Suppressing wraparound artifacts of
Up: Fourier approach
Previous: Fourier approach
Stanford Exploration Project
7/5/1998
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , the shallow part of
the data gets severely compressed in the t2 grid. The amount of
compression can lead to inadequate sampling, and as a result, aliasing
artifacts in the frequency domain. Moreover, it can be difficult to
recover from the loss of information in the transformed domain when
transforming back into the original grid. A partial remedy for this
problem is to increase the grid size in the t2 domain. The top plots
in Figure
, the shallow part of
the data gets severely compressed in the t2 grid. The amount of
compression can lead to inadequate sampling, and as a result, aliasing
artifacts in the frequency domain. Moreover, it can be difficult to
recover from the loss of information in the transformed domain when
transforming back into the original grid. A partial remedy for this
problem is to increase the grid size in the t2 domain. The top plots
in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show the result of back transformation to
the t grid and the difference between this result and the original
model (plotted on the same scale). We can see a noticeable loss of
information in the upper (shallow) part of the data, caused by
undersampling. The bottom plots in Figure
show the result of back transformation to
the t grid and the difference between this result and the original
model (plotted on the same scale). We can see a noticeable loss of
information in the upper (shallow) part of the data, caused by
undersampling. The bottom plots in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) correspond
to increasing the grid size by a factor of three. Some of the
artifacts have been suppressed, at the expense of dealing with a
larger grid.
correspond
to increasing the grid size by a factor of three. Some of the
artifacts have been suppressed, at the expense of dealing with a
larger grid.
